Ecuaciones del Círculo
Es fácil hacer un círculo:
Dibuja una curva que esté a un "radio" de distancia de un punto central.
De modo que:
Todos los puntos están a la misma distancia del centro.
De hecho la definición de un círculo es
Círculo: Es el conjunto de todos los puntos en un plano que están a una distancia fija de un punto central.
El Círculo en una Gráfica
Pongamos un círculo de radio 5 en una gráfica:
Ahora veamos exactamente dónde están todos los puntos.
Hacemos un triángulo rectángulo:
Y luego usamos Pitágoras:
x2 + y2 = 52
Hay un número infinito de esos puntos. Aquí unos ejemplos:
| x | y | x2 + y2 |
|---|---|---|
| 5 | 0 | 52 + 02 = 25 + 0 = 25 |
| 3 | 4 | 32 + 42 = 9 + 16 = 25 |
| 0 | 5 | 02 + 52 = 0 + 25 = 25 |
| −4 | −3 | (−4)2 + (−3)2 = 16 + 9 = 25 |
| 0 | −5 | 02 + (−5)2 = 0 + 25 = 25 |
En todos los casos, un punto en el círculo sigue la regla x2 + y2 = radio2
Podemos usar esa idea para encontrar un valor faltante.
Ejemplo: x tiene coordenada 2 y el radio es 5
(El ± significa que hay dos posibles valores: uno con + y el otro con −)
Y aquí están los dos puntos:
Un caso más general
Ahora pongamos el centro en (a,b)
Entonces el círculo es todos los puntos (x,y) que están "r" alejados del centro (a, b).
Ahora veamos dónde están los puntos (usando un triángulo rectángulo y Pitágoras):
Es la misma idea que antes, pero necesitamos restar a y b:
(x−a)2 + (y−b)2 = r2
¡Y ésa es la "Forma Estándar" para la ecuación de un círculo!
Muestra toda la información importante de un vistazo: el centro (a,b) y el radio r.
Ejemplo: Un círculo con centro en (3,4) y radio 6:
Empieza con:
(x−a)2 + (y−b)2 = r2
Sustituye (a,b) y r:
(x−3)2 + (y−4)2 = 62
Entonces podemos usar nuestras habilidades de álgebra para simplificar y reorganizar esa ecuación, dependiendo de para qué la necesitemos.
Inténtalo tú mismo
"Forma General"
¡Puedes estar viendo la ecuación de un círculo y no saberlo!
Debido a que puede no estar en la "forma estándar" de arriba.
Como ejemplo, pongamos algunos valores de a, b y r y luego desarrollemos
Y al final nos queda:
x2 + y2 − 2x − 4y − 4 = 0
Es la ecuación de un círculo, ¡pero "disfrazada"!
Entonces, cuando veas algo así, piensa "hmm ... ¡eso podría ser
un círculo!"
De hecho, podemos escribirlo en "Forma General" poniendo
constantes en lugar de los números:
x2 + y2 + Ax + By + C = 0
Nota: la forma general siempre tiene x2 + y2
como sus dos primeros términos.
Pasando de la Forma General a la Forma Estándar
Ahora imagina que tenemos una ecuación en su Forma General:
x2 + y2 + Ax + By + C = 0
¿Cómo podemos ponerla en su Forma Estándar, como ésta que sigue?
(x-a)2 + (y-b)2 = r2
La respuesta es completando el cuadrado (lee sobre eso) dos veces... una para x y la otra para y:
Ejemplo: x2 + y2 − 2x − 4y − 4 = 0
Ahora completa el cuadrado para x (toma la mitad del -2, elévalo al cuadrado y súmalo a ambos lados):
(x2 - 2x + (-1)2) + (y2 - 4y) = 4 + (-1)2
Y completa el cuadrado para y (toma la mitad del -4, elévalo al cuadrado y súmalo a ambos lados):
(x2 - 2x + (-1)2) + (y2 - 4y + (-2)2) = 4 + (-1)2 + (-2)2
Pon algo de orden:
¡Y ahora está en Forma Estándar!
(Nota: este ejemplo utilizó el ejemplo a=1, b=2, r=3 de antes, ¡así que lo hicimos bien!)
Círculo Unitario
Si colocamos el centro del círculo en (0,0) y establecemos el radio en 1 obtenemos:
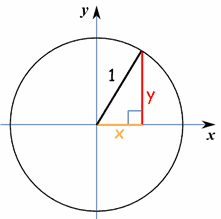 |
(x-a)2 + (y-b)2 = r2 (x-0)2 + (y-0)2 = 12 x2 + y2 = 1 La cual es la ecuación del Círculo Unitario |
Cómo Graficar un Círculo Manualmente
1. Ubica y marca el centro (a,b)
2. Señala 4 puntos a un "radio" de distancia del centro hacia arriba, abajo, izquierda y derecha.
3. ¡Dibuja sobre esos 4 puntos!
Ejemplo: Graficar (x-4)2 + (y-2)2 = 25
La fórmula para un círculo es (x−a)2 + (y−b)2 = r2
Así que el centro está en (4,2)
Y r2 es 25, de modo que el radio mide √25 = 5
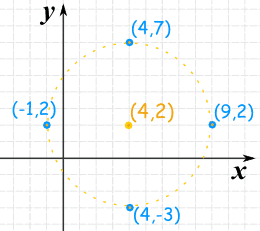
Así que podemos trazar
- El centro: (4,2)
- Arriba: (4,2+5) = (4,7)
- Abajo: (4,2-5) = (4,-3)
- Izquierda: (4-5,2) = (-1,2)
- Derecha: (4+5,2) = (9,2)
¡Ahora dibujemos el círculo lo mejor que podamos!
Cómo trazar un círculo en la computadora
Necesitamos reorganizar la fórmula para obtener "y ="
Deberíamos terminar con dos ecuaciones (arriba y abajo del círculo) que luego se pueden trazar.
Ejemplo: Grafica (x−4)2 + (y−2)2 = 25
El centro está en (4,2), y el radio mide √25 = 5
Re-acomoda para obtener "y=":
¡puede haber dos raíces!) Mueve el "−2" a la derecha:y = 2 ± √[25 − (x−4)2]
Entonces, cuando graficamos estas dos ecuaciones, deberíamos tener un círculo:
- y = 2 + √[25 − (x−4)2]
- y = 2 − √[25 − (x−4)2]
Echa un vistazo a la gráfica de esta ecuación.
También es posible usar nuestro graficador de ecuaciones para hacerlo todo en un solo paso.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

