Modelos Matemáticos
Las matemáticas se pueden usar para "modelar", o representar, cómo funciona el mundo real.
Ejemplo: ¿cuánto espacio hay dentro de esta caja de cartón?
Conocemos tres medidas:
- l (longitud),
- p (profundidad), y
- a (altura),
y la fórmula para el volumen de un cuboide es:
Volumen = l × p × a
Entonces tenemos un modelo matemático (muy simple) del espacio en esa caja.
¿Preciso?
El modelo no es exactamente lo mismo que lo real.
En nuestro ejemplo, no pensamos en el grosor del cartón ni en muchas otras cosas del "mundo real".
Pero espero que sea lo suficientemente bueno como para ser útil.
 |
Si se nos cobra por el volumen de la caja que enviamos, podemos
tomar algunas medidas y saber cuánto pagar. También puede ser útil al decidir qué caja comprar cuando necesitamos empacar cosas. ¡Entonces el modelo es útil!
|
Pero tal vez necesitamos más precisión. Podríamos tener que enviar cientos de cajas todos los días, y el grosor del cartón es importante. Entonces, veamos si podemos mejorar el modelo:
El cartón tiene grosor "g", y todas las medidas están por fuera de la caja ... ¿Cuánto espacio hay dentro?
The inside measurements need to be reduced by the thickness of each side:
- La longitud interior es l−2g
- La profundidad interior es p−2g,
- La altura interior es a−2g
y ahora la fórmula es:
Volumen interno = (l−2g) × (p−2g) × (a−2g)
Ahora tenemos un mejor modelo. Todavía no es perfecto (no consideramos el espacio desperdiciado por si no pudiéramos empacar las cosas de forma compacta y ordenada, etc.), pero es mejor.
Entonces, un modelo no representa exactamente la realidad, pero debería ser lo suficientemente bueno como para ser útil.
Jugando con el modelo
Ahora que tenemos un modelo, podemos usarlo de diferentes maneras:
Ejemplo: tu empresa utiliza cajas de 200x300x400mm y el cartón tiene 5mm de espesor. Alguien sugiere usar cartón de 4 mm ... ¿cuánto mejor sería eso?
Comparemos los dos volúmenes:
- Volumen actual = (200-2×5) × (300-2×5) × (400-2×5) = 21,489,000 mm3
- Nuevo volumen = (200-2×4) × (300-2×4) × (400-2×4) = 21,977,088 mm3
Ése es un cambio de:
(21,977,088-21,489,000)/21,489,000 ≈ 2% más volumen
Pero todavía hay cosas del "mundo real" en las que pensar, como: "¿será lo suficientemente resistente?"
Pensando con claridad
¡Para establecer un modelo matemático también necesitamos pensar claramente sobre los datos!
Ejemplo: en nuestra calle hay el doble de perros que de gatos. ¿Cómo escribimos esto como una ecuación?
- Sea P = número de perros
- Sea G = número de gatos
Ahora....eso es: 2P = G
¿ O debería ser: P = 2G ?
¡Piensa cuidadosamente ahora!
La respuesta correcta es P = 2G
(2P = G es un error común, ya que la pregunta está escrita "dos veces ... perros ... gatos")
Aquí hay otro:
Ejemplo: eres es el supervisor de los trabajadores de un turno de 8 horas. Recientemente, sus tiempos de descanso se redujeron en 10 minutos, pero la producción total no mejoró.
A primera vista no hay nada que modelar, porque no hubo cambios en la producción.Pero espera un minuto ... están trabajando 10 minutos más, pero producen la misma cantidad, ¡así que la producción por hora debe haber disminuido!
Supongamos que solían trabajar 7 horas (420 minutos):
Cambio en la producción por hora = 410/420 = 0.976...
Lo cual es una reducción de más del 2%
Pero aún peor: las primeras horas del turno no se ven afectadas por el tiempo de descanso más corto, por lo que podría ser una reducción del 4 ó 5% más adelante en el turno.Podrías recomendar:
- mirar las tasas de producción por cada hora del turno
- probar diferentes tiempos de descanso para ver cómo afectan la producción
Un ejemplo más grande: el tamaño más económico
Bien, intentemos construir y usar un modelo matemático para resolver una pregunta del mundo real.
¡Tu empresa va a hacer sus propias cajas!
Se ha decidido que la caja debe contener 0.02m3
(0.02 metros cúbicos, que equivalen a 20 litros) de tuercas y
tornillos.
La caja debe tener una base cuadrada y doble espesor en la parte
superior e inferior.
El cartón cuesta $0.30 por metro cuadrado.
Depende de ti decidir el tamaño más económico.
Paso 1: ¡Haz un dibujo!
¡Ayuda dibujar lo que estamos tratando de resolver!
| La base es cuadrada, así que usaremos "l" para ambas longitudes |
La caja tiene 4 lados y tapas y fondos dobles. La forma de la caja podría cortarse así (pero probablemente sea más complicada): |
Paso 2: ¡Escribe una fórmula!
Ignorando el grosor para este modelo:
Volumen = l × l × a = l2a
Y nos dicen que el volumen debe ser 0.02m3:
l2a = 0.02
Áreas:
Área de los 4 lados = 4 × l × a = 4la
Área de las partes dobles (base y tapa) = 4 × l × l = 4l2
Total de cartón necesario:
Área de cartón = 4la + 4l2
Paso 3: haz una fórmula única para el costo
Queremos una fórmula única para el costo:
Costo = $0.30 × Área de cartón
= $0.30 × (4la + 4l2)
Y ése es el costo cuando conocemos la longitud y la altura.Podría ser difícil trabajar con ... una función con dos variables.
¡Pero podemos hacerlo más simple! Como la longitud y la altura ya están relacionados por el volumen:
Volumen = l2a = 0.02
... que se puede reorganizar a ...
a = 0.02/l2
... y eso se puede incluir en la fórmula del costo ...
Costo = $0.30 × (4p×0.02/l2 + 4l2)
Y ahora el costo está relacionado directamente con la longitud solamente.Con una pequeña simplificación obtenemos:
Costo = $0.30 × (0.08/l+ 4l2)
Paso 4: haz una gráfica y encuentra el costo mínimo
¿Qué graficar? Bueno, la fórmula solo tiene sentido para longitudes mayores que cero, y también descubrí que para longitudes superiores a 0.5 el costo se vuelve cada vez más grande.Así que aquí hay una gráfica de esa fórmula de costo para longitudes entre 0.0m y 0.55m:
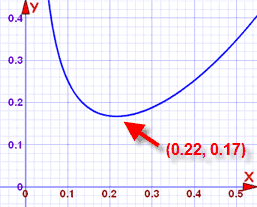
Gráfica de y= 0.3(0.08/x+4x2)
x es la longitud, y y es el costo
Solo a simple vista, veo que el costo alcanza un mínimo de aproximadamente (0.22, 0.17). En otras palabras:
- Cuando la longitud es aproximadamente 0.22 m (valor de x),
- el costo mínimo es aproximadamente $0.17 por caja (valor de y).
De hecho, mirando la gráfica, el ancho podría estar entre 0.20 y 0.24 sin afectar mucho el costo mínimo.
Paso 5: recomendaciones
Usando este modelo matemático ahora puedes recomendar:
- Longitud = 0.22 m
- Altura = 0.02/l2 = 0.02/0.222 = 0.413m
- Costo = $0.30 × (0.08/l+ 4l2) = $0.30 × (0.08/0.22+ 4×0.222) = $0.167
Pero cualquier ancho entre 0.20m y 0.24m está bien.
Tal vez te gustaría sugerir mejoras a este modelo:
- Incluye el costo de pegamento/grapas y ensamblaje
- Incluye el desperdicio al cortar la caja de cartón.
- ¿Es esta caja una buena forma para empacar, manipular y almacenar?
- ¡Cualquier otra idea que puedas tener!
Prediciendo el futuro
Los modelos matemáticos también se pueden usar para pronosticar el comportamiento futuro.
Ejemplo: una empresa de helados realiza un seguimiento de cuántos helados se venden en diferentes días.

Luego pueden predecir las ventas futuras en función del pronóstico del tiempo y decidir cuántos helados necesitan hacer ... ¡con anticipación!
Modelado por computadora
Los modelos matemáticos pueden volverse muy complejos y, por lo tanto, las reglas matemáticas a menudo se escriben en programas de computadora para hacer un modelo de computadora.
Juega con un sencillo modelo
computacional de la reflexión dentro de una elipse
o con esta animación de un
péndulo doble.
Algunos ejemplos más complejos incluyen:
- Predicción del tiempo
- Modelos económicos (predicción de tasas de interés, desempleo, etc.)
- Modelos de cómo se comportan las grandes estructuras bajo tensión (puentes, rascacielos, etc.)
- Mucho más ...
