Propiedad del Producto Cero
La "Propiedad del Producto Cero" dice que:
Si a × b = 0
entonces a = 0 o
b = 0
(o ambos a = 0 y b = 0)
Puede ayudarnos a resolver ecuaciones:
Ejemplo: Resolver (x−5)(x−3) = 0
La "propiedad del producto cero" dice:
Si (x−5)(x−3) = 0 entonces (x−5) = 0 o (x−3) = 0
Ahora solo resolvemos cada uno de esos:
Para (x−5) = 0 se tiene x = 5
Para (x−3) = 0 se tiene x = 3
Y las soluciones son:
x = 5, o x = 3
Aquí está en una gráfica:
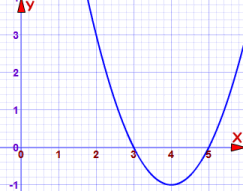
y=0 cuando x=3 o x=5
Forma estándar de una ecuación
A veces podemos resolver una ecuación poniéndola en forma estándar y luego usando la propiedad del producto cero:
La "Forma Estándar" de una ecuación es:
(alguna expresión) = 0
En otras palabras, "= 0" está a la derecha y todo lo demás está a la izquierda.
Ejemplo: Pon x2 = 7 en Forma Estándar
Respuesta:
x2 − 7 = 0
Forma estándar y propiedad del producto cero
Vamos a probar:
Ejemplo: Resolver 5(x+3) = 5x(x+3)
Es tentador dividir por (x + 3), pero eso es dividir entre cero cuando x = −3
Entonces, en su lugar, podemos usar la "Forma Estándar":
5(x+3) − 5x(x+3) = 0
Que se puede simplificar a:
(5−5x)(x+3) = 0
5(1−x)(x+3) = 0
Entonces la "Propiedad del Producto Cero" dice:
(1−x) = 0, o (x+3) = 0
Y las soluciones son:
x = 1, o x = −3
Y otro ejemplo:
Ejemplo: Resolver x3 = 25x
Es tentador dividir por x, pero eso es dividir entre cero cuando x = 0
Entonces usemos la forma estándar y la propiedad del producto cero.
Pasa todo al lado izquierdo:
x3 − 25x = 0
Factoriza la x:
x(x2 − 25) = 0
x2 − 25 es una diferencia de cuadrados, y puede factorizarse como (x − 5)(x + 5):
x(x − 5)(x + 5) = 0
Ahora podemos ver tres formas posibles en que podría terminar en cero:
x = 0, o x = 5, o x = −5
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
