Derivatives
Derivatives are all about change ...
Let us get straight into an example: the function x2:
f(x) = x2
Here are some values:
|
 |
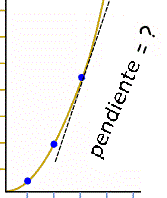 |
As x increases, so does f(x) ... but how fast? Can we find the slope (or rate of change) at any point? With Derivatives we can! The derivative gives ... |
Slope
The slope (or gradient) of a line is simply:
| Slope = |
|
So, let us set about calculating the "differences"
Differences
The symbol for difference is the greek letter "delta": "Δ" Example: if t goes from 3 to 3.1, then Δt=0.1 |
Here are some differences for x and f(x)
| x | Δx | f(x) | Δf(x) |
|---|---|---|---|
| 0 | 0 | ||
| 0.5 | 0.5 | 0.25 | 0.25 |
| 1 | 0.5 | 1 | 0.75 |
| 1.5 | 0.5 | 2.25 | 1.25 |
| 2 | 0.5 | 4 | 1.75 |
| 2.5 | 0.5 | 6.25 | 2.25 |
The table shows that, for example, between 1.5 and 2 f(x) grew by 1.75
I kept Δx at 0.5, but Δf(x) is getting larger and larger, meaning the rate of change is increasing.
But now we introduce the first of our important steps:
1. Make a Formula
Instead of long tables of numbers, we want a formula for calculating Δf(x).
What happens between x and x+Δx?
| At x: | At x+Δx: | |
| f (x) = x2 | f (x+Δx) = (x + Δx)2 | |
| So, the difference is: | ||
| Δf(x) = f (x + Δx) - f (x) | ||
| = (x + Δx)2 − x2 | ||
2. Simplify Formula
| We can expand "(x + Δx)2": | Δf(x) = x2 + 2x Δx + Δx2 − x2 | |
| And then simplify the formula: | Δf(x) = |
Now we can calculate Δf(x) in one go:
Example: What is Δf(x) for x=1.5 and Δx=0.5 ?
Δf(x) = 2 x Δx + (Δx)2
= 2 × 1.5 × 0.5 + 0.5 × 0.5 = 1.5 + 0.25 = 1.75
That tells us how much f(x) changes, but not how fast. We still need to compare it to the change in x.
 |
Example: if my weight increased by 1kg, was that fast or slow? You can only answer if you know how long it took to increase. If it happened in 1 day, then it is fast, but if it took 1 year, it is slow. |
3. Rate of Change
To work out how fast (called the rate of change) we divide by Δx:
Rate of change = Δf(x) / Δx
That tells us "how much f(x) changes for every change in x"
The Rate of Change can be seen as the slope of a line:
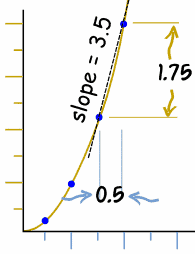 |
In our x2 example, this becomes: Δf(x) / Δx = Example: What is the rate of change for Δf(x) when x=1.5 and Δx=0.5 ? Rate of change = Δf(x) / Δx = ( 2 x Δx + (Δx)2 ) / Δx = (2 × 1.5 × 0.5 + 0.52)/0.5 = 1.75/0.5 = 3.5 This tells us the slope of the line between x and (x+Δx). |
But Not At A Point
But it doesn't yet tell us the slope at any specific point ... ... for example what is the slope at 1.5? But we can find the slope at a point if we: Reduce Δx towards 0. That will show us the slope just where 1.5 is.
|
 |
However, Δx can't be 0, because dividing by 0 is wrong! ...
... and a point can't really have a slope (imagine a nail through a piece of wood - the wood could spin around in any direction) ...
... but we can try getting closer and closer:
| Δx = 0.5: Rate of change (we already calculated) = 3.5 | |
| Δx = 0.05: Rate of change = (2 × 1.5 × 0.05 + 0.052)/0.05 = 0.1525/0.05 = 3.05 | |
| Δx = 0.005: Rate of change = (2 × 1.5 × 0.005 + 0.0052)/0.005 = 3.005 | |
We seem to be heading for Rate of change = 3 |
4. Use Limits to get Δx close to 0
In fact we just used the idea of limits to find the Rate of Change!
Because we weren't allowed to have Δx = 0, we tried approaching it closer and closer.
So let's try putting our Rate of Change formula into a limit, and see what we get:
![]()
The first thing we can do is simplify it, because Δx is at both the top and bottom:
![]()
Now, as Δx goes towards zero we have:
![]()
And that is it ... the rate of change (the slope of the line) is simply 2x
We have solved it! We can find the slope of the line at any point.
The slope at 1.5 is 2 × 1.5 = 3, ... the slope at 10 is 2 × 10 = 20, etc ...
And even better, we have done our first derivative!
Those Steps Again
So how did we do this again?
- We wrote a formula for Δf(x) = f(x+Δx) - f(x)
- We simplified that formula (to "2x Δx + Δx2")
- We divided that by Δx to get the rate of change
- We used limits to get Δx close to 0.
Definition of a Derivative
Let us now imagine that f(x) is any function, and follow the steps:
1. A formula for Δf(x)
Δf(x) = f(x+Δx) - f(x)
2. Simplify
(can't simplify in this case)
3. Divide by Δx to get the rate of change
Δf(x)/Δx = (f(x+Δx) - f(x))/Δx
4. Use limits to get Δx close to 0.
![]()
And that is the Defintion of a Derivative, for which we often use the little prime mark (') as shown.
Try It On Another Function
Let's try x3
A formula for Δf(x)
Δf(x) = f(x+Δx) - f(x) = (x+Δx)3 − x3
Simplify
(x+Δx)3 − x3 = x3 + 3x2Δx + 3xΔx2 + Δx3 − x3
= 3x2Δx + 3xΔx2 + Δx3
Divide by Δx to get the rate of change
Δf(x)/Δx = (3x2Δx + 3xΔx2 + Δx3)/Δx
Use limits to get Δx close to 0.
We can simplify it, then work out what happens when Δx goes towards 0:
So the derivative of x3 is 3x2
Other Notations
Sometimes the derivative is written like this:
![]()
![]()
We will explore that way of working on Derivatives as dy/dx

