La Media en una Tabla de Frecuencias
Es fácil calcular la Media:
Suma todos los números,
luego divide entre cuántos números hay.
Ejemplo: ¿Cuál es la media de estos números?
6, 11, 7
- Suma los números: 6 + 11 + 7 = 24
- Divide entre cuántos números hay (hay 3 números): 24 ÷ 3 = 8
La media es 8
Pero a veces no tenemos una simple lista de números, sino que podría ser una tabla de frecuencias como esta (la "frecuencia" indica con qué frecuencia ocurren):
| Puntaje | Frecuencia |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 4 |
| 4 | 2 |
| 5 | 1 |
(dice que el puntaje 1 ocurrió 2 veces, el puntaje 2 ocurrió 5 veces, y así sucesivamente)
Podríamos listar todos los números así:
Media = 1+1 + 2+2+2+2+2 + 3+3+3+3 + 4+4 + 5(cuántos números hay)
Pero en lugar de hacer muchas sumas (como 3+3+3+3) es más fácil usar la multiplicación:
Media = 2×1 + 5×2 + 4×3 + 2×4 + 1×5(cuántos números hay)
Y en lugar de contar cuántos números hay, podemos sumar las frecuencias:
Media = 2×1 + 5×2 + 4×3 + 2×4 + 1×52 + 5 + 4 + 2 + 1
Así que ahora calculamos:
Media = 2 + 10 + 12 + 8 + 514
= 3714 = 2.64...
¡Y así es como se calcula la media a partir de una tabla de frecuencias!
Aquí hay otro ejemplo:
Ejemplo: Espacios de estacionamiento por casa en la Calle Hampton
Isabel recorrió la calle para averiguar cuántos espacios de estacionamiento tiene cada casa. Aquí están sus resultados:
| Espacios de estacionamiento |
Frecuencia |
|---|---|
| 1 | 15 |
| 2 | 27 |
| 3 | 8 |
| 4 | 5 |
¿Cuál es el promedio de espacios de estacionamiento?
Respuesta:
La media es 2.05 (a 2 decimales)
(¡mucho más fácil que sumar todos los números por separado!)
Notación
Ahora que sabes cómo se hace, hagamos ese último ejemplo de nuevo, pero usando fórmulas.
(lee más en Notación Sigma)
(donde f es la frecuencia)
Y podemos usarlo así:
Del mismo modo podemos sumar "frecuencia por puntaje" de esta manera:
(donde f es la frecuencia y x es el puntaje correspondiente)
Y la fórmula para calcular la media de una tabla de frecuencias es:
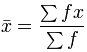
La x con la barra encima representa "la media de x"
Así que ahora estamos listos para hacer nuestro ejemplo anterior, pero con la notación correcta.
Ejemplo: Calcula la media de esta tabla de frecuencias
| x | f |
|---|---|
| 1 | 15 |
| 2 | 27 |
| 3 | 8 |
| 4 | 5 |
Y aquí está:
¡Ahí lo tienes! Ya puedes usar la notación sigma.
Calcular en la tabla
A menudo es mejor hacer los cálculos en la tabla.
Ejemplo: (continuación)
Del ejemplo anterior, calcula f × x en la columna de la derecha y luego calcula los totales:
| x | f | fx |
|---|---|---|
| 1 | 15 | 15 |
| 2 | 27 | 54 |
| 3 | 8 | 24 |
| 4 | 5 | 20 |
| TOTALES: | 55 | 113 |
Y la media es entonces fácil:
Media de x = 11355 = 2.05...