Solución de los botes y lápices

Ir directo a la respuesta El problema 1 se puede resolver simplemente probando con unos cuantos números, claro. Pero si queremos resolver el problema 2 lo tenemos más difícil. Lo que vamos a hacer es resolver el problema 1 con un poco de álgebra. Cuando entiendas las matemáticas que usamos puedes probar a resolver el problema 2 de la misma manera.

Lo primero es leer con cuidado el problema.

Problema 1

Tengo unos cuantos lápices y botes.
Si pongo 4 lápices en cada bote me queda un bote de sobra.
Si pongo 3 lápices en cada bote me sobra un lápiz.
¿Cuántos lápices y botes tengo?

Aquí hay dos afirmaciones distintas. Vamos con la primera.

Cuando hay cuatro lápices en cada bote hay un bote de más. O sea que el número de botes es igual al número de lápices entre cuatro más otro bote.

Esto lo podemos escribir usando el álgebra.

b = (l ÷ 4) + 1

Ahora mira la segunda afirmación.

Cuando hay tres lápices por bote sobra un lápiz. Antes hemos escrito una fórmula para el número de botes. Ahora tenemos que calcular el número de lápices. Podemos decir que el número de lápices es igual al número de botes por tres más un otro lápiz.

Usando otra vez el álgebra escribimos

l = 3b + 1

Al final tenemos dos ecuaciones lineales. Hay dos maneras de resolverlas. Gráficamente, o con ecuaciones simultáneas. Aquí lo haremos con un gráfico.

Primero reordenamos las fórmulas para que empiecen por b.

b = (l ÷ 4) + 1 (ecuación 1)

b = (l − 1) ÷ 3 (ecuación 2)

Las dibujamos en un gráfico usando x=l e y=b;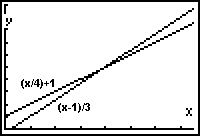
Si encontramos el punto de intersección tendremos la respuesta.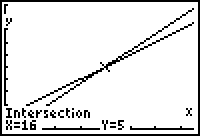

Así que hay 16 lápices y 5 botes.