Proporciones
Una proporción dice que dos razones (o fracciones) son iguales en valor.
Ejemplo:
Vemos que 1 de cada 3 es igual a 2 de cada 6.
Las razones son las mismas, así que están en proporción.
Ejemplo: Cuerda
La longitud y el peso de una cuerda están en proporción.
Si 20m de cuerda pesan 1kg, entonces:
- 40m de esa cuerda pesan 2kg
- 200m de esa cuerda pesan 10kg
- y así sucesivamente
Entonces:
201 = 402
Tamaños
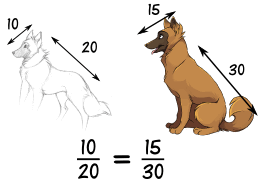
Cuando las formas están "en proporción", sus tamaños relativos son los mismos.
Aquí vemos que las razones entre la longitud de la cabeza y la del cuerpo son las mismas en ambos dibujos.
Por lo tanto, son proporcionales.
¡Hacer la cabeza demasiado larga o corta se vería mal!
Ejemplo: Los tamaños de papel internacionales (como A3, A4, A5, etc.) tienen todos las mismas proporciones:
Así que cualquier diseño o documento puede redimensionarse para encajar en cualquier hoja. Muy práctico.
Trabajando con proporciones
AHORA, ¿cómo usamos esto?
Ejemplo: quieres dibujar la cabeza del perro... ¿qué tan larga debe ser?
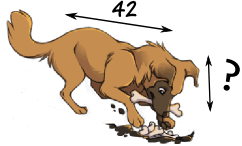
Escribamos la proporción con la ayuda de la razón 10/20 de arriba:
?42 = 1020
Ahora lo resolvemos usando un método especial:
Multiplica en cruz los valores conocidos,
luego divide por el tercer número
Y obtenemos esto:
? = (42 × 10) / 20
= 420 / 20
= 21
Así que deberías dibujar la cabeza con una longitud de 21.
Uso de proporciones para resolver porcentajes
¡Un porcentaje es en realidad una razón! Decir "25%" es en realidad decir "25 por cada 100":
25% = 25100
Podemos usar proporciones para resolver preguntas que involucran porcentajes.
El truco es poner lo que sabemos en esta forma:
ParteTotal = Porcentaje100
Ejemplo: ¿cuánto es el 25% de 160?
El porcentaje es 25, el total es 160, y queremos hallar la "parte":
Parte160 = 25100
Multiplica en cruz los valores conocidos, luego divide por el tercer número:
Parte = (160 × 25) / 100
= 4000 / 100
= 40
Respuesta: El 25% de 160 es 40.
Nota: también podríamos haber resuelto esto haciendo la división primero, así:
Parte = 160 × (25 / 100)
= 160 × 0.25
= 40
Cualquier método funciona bien.
También podemos encontrar un porcentaje:
Ejemplo: ¿cuánto es $12 como porcentaje de $80?
Rellena lo que sabemos:
$12$80 = Porcentaje100
Multiplica en cruz los valores conocidos, luego divide por el tercer número. Esta vez los valores conocidos en diagonal son el de arriba a la izquierda y el de abajo a la derecha:
Porcentaje = ($12 × 100) / $80
= 1200 / 80
= 15%
Respuesta: $12 es el 15% de $80
O hallar el Total:
Ejemplo: El precio de oferta de un teléfono fue de $150, que era solo el 80% del precio normal. ¿Cuál era el precio normal?
Rellena lo que sabemos:
$150Total = 80100
Multiplica en cruz los valores conocidos, luego divide por el tercer número:
Total = ($150 × 100) / 80
= 15000 / 80
= 187.50
Respuesta: el precio normal del teléfono era $187.50
Uso de proporciones para resolver triángulos
Podemos usar proporciones para resolver triángulos semejantes.
Ejemplo: ¿Qué altura tiene el árbol?
Miguel intentó usar una escalera, cinta métrica, cuerdas y varias otras cosas, pero aún así no lograba calcular la altura del árbol.
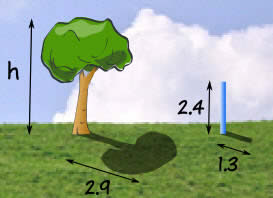
Pero entonces Miguel tiene una idea brillante... ¡triángulos semejantes!
Miguel mide un palo y su sombra (en metros), y también la sombra del árbol, y esto es lo que obtiene:

Ahora Miguel hace un boceto de los triángulos y anota la razón "Altura a Longitud" para ambos triángulos:
Altura:Longitud de sombra: h2.9 m = 2.4 m1.3 m
Multiplica en cruz los valores conocidos, luego divide por el tercer número:
h = (2.9 × 2.4) / 1.3
= 6.96 / 1.3
= 5.4 m (al 0.1 más cercano)
Respuesta: el árbol mide 5.4 m de altura.
¡Y ni siquiera necesitó una escalera!
La "Altura" podría haber estado en la parte inferior, siempre y cuando estuviera en la parte inferior en AMBAS razones, así:

Probemos con la razón de "Longitud de sombra a Altura":
Longitud de sombra:Altura: 2.9 mh = 1.3 m2.4 m
Multiplica en cruz los valores conocidos, luego divide por el tercer número:
h = (2.9 × 2.4) / 1.3
= 6.96 / 1.3
= 5.4 m (al 0.1 más cercano)
Es el mismo cálculo que antes.
Un ejemplo "concreto"
¡Las razones pueden tener más de dos números!
Por ejemplo, el concreto se hace mezclando cemento, arena, piedras y agua.

Una mezcla típica de cemento, arena y piedras se escribe como una razón, como 1:2:6.
Podemos multiplicar todos los valores por la misma cantidad y seguir teniendo la misma razón.
10:20:60 es lo mismo que 1:2:6
Así que cuando usamos 10 cubetas de cemento, debemos usar 20 de arena y 60 de piedras.
Ejemplo: acabas de poner 12 cubetas de piedras en una mezcladora, ¿cuánto cemento y cuánta arena deberías añadir para hacer una mezcla 1:2:6?
Organicémoslo en una tabla para que sea más claro:
| Cemento | Arena | Piedras | |
|---|---|---|---|
| Razón necesaria: | 1 | 2 | 6 |
| Tienes: | 12 |
Tienes 12 cubetas de piedras, pero la razón dice 6.
No pasa nada, simplemente tienes el doble de piedras que el número de la razón... así que necesitas el doble de todo para mantener la proporción.
Aquí está la solución:
| Cemento | Arena | Piedras | |
|---|---|---|---|
| Razón necesaria: | 1 | 2 | 6 |
| Tienes: | 2 | 4 | 12 |
Y la razón 2:4:12 es la misma que 1:2:6 (porque muestran los mismos tamaños relativos).
Así que la respuesta es: añade 2 cubetas de cemento y 4 cubetas de arena. (También necesitarás agua y remover mucho....)
¿Por qué son la misma razón? Bueno, la razón 1:2:6 dice que hay que tener:
- el doble de arena que de cemento (1:2:6)
- 6 veces más piedras que cemento (1:2:6)
En nuestra mezcla tenemos:
- el doble de arena que de cemento (2:4:12)
- 6 veces más piedras que cemento (2:4:12)
¡Así que debería estar justo en su punto!
Eso es lo bueno de las razones. Puedes hacer las cantidades más grandes o más pequeñas y, mientras los tamaños relativos sean los mismos, la razón seguirá siendo la misma.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

