Soluciones Aproximadas
A veces es difícil resolver una ecuación exactamente. ¡Pero una respuesta aproximada puede ser lo suficientemente buena!
¿Qué es lo suficientemente bueno?
Bueno, eso depende de lo que estés trabajando.
- Si estás tratando con millones de dólares, entonces deberías tratar de acercarte bastante. Eso podría necesitar muchos dígitos significativos.
- Si estás calculando cuánta comida comprar para una fiesta, entonces un pequeño error no importará tanto. Siempre puedes comprar un poco más para estar seguro.
- O algo intermedio.
Entonces, comprender en qué estás trabajando te ayuda a saber qué tan preciso debes ser.
Ejemplo: Cocina
En la cocina en general podemos cambiar algunas cosas y no pasa nada. Agregar 50 gramos extra de zanahoria está bien. ¡Solo no demasiada sal, por favor!

Ejemplo: Repostería
Al hornear un pastel, los cambios pequeños en los ingredientes suelen estar bien; un poco más de cacao o un poco menos de azúcar no es problema, pero si nos excedemos, el resultado puede ser un fracaso.
Agregar 100 ml de leche extra probablemente hará que el resultado quede húmedo y desagradable.
Ejemplo: Ingeniería Aeroespacial
Los cálculos de la trayectoria y de las necesidades de combustible de las naves espaciales requieren una precisión extrema. Pequeños errores pueden provocar desviaciones de la ruta y el fracaso de la misión.
Resolver Ecuaciones
Para ayudar a reducir el error, al resolver ecuaciones:
- primero resuelve para x = algo
- después haz las operaciones
De la siguiente forma:
Ejemplo: Resuelve x/7 − 6.3068 + 2π = 0 (a 3 decimales)
¿Por qué esperar hasta el final para hacer los cálculos? Bueno, cada vez que haces una operación puedes introducir un error. Si haces esto varias veces, tus errores pueden acumularse y ser bastante grandes.
Comprobación
Si tu respuesta es aproximada, tu comprobación también será aproximada.
Ejemplo: Comprueba que x = 0.165 es solución de x/7 − 6.3068 + 2π = 0
No del todo correcto, pero muy cerca.
Estimación Gráfica
Puedes hacer buenas aproximaciones usando gráficas, particularmente usando la función de zoom, como en nuestro graficador de funciones.
Aquí te va un ejemplo:
Ejemplo: estima la solución de x3 − 2x2 − 1 = 0 (a 2 decimales).
Solución: ¡Grafiquemos!
Aquí está mi primer intento. Puedo ver que cruza y = 0 a aproximadamente en x = 2.2
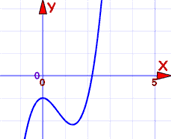
Acerquemos el zoom para ver si podemos definir de forma más precisa el punto de cruce:
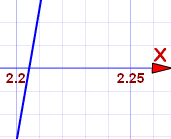
Cruza entre 2.20 y 2.21 ... un poco más cerca de 2.21. Se nos solicitan 2 decimales, por lo que nuestra respuesta es:
x3 − 2x2 − 1 = 0 cerca de x = 2.21
Comprobación: (2.21)3 − 2(2.21)2 + 2 = aproximadamente 0.025, cerca de y=0
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
