Hexágono Mágico Para Identidades Trigonométricas
Nota: La función Seno se abrevia tanto
sen como sin
| Este hexágono es un diagrama especial para ayudarte a recordar algunas Identidades Trigonométricas |
Dibuja el diagrama cuando estés batallando con las identidades trigonométricas ... ¡puede ayudarte! Aquí te digo cómo:
Construyámoslo: las identidades de cociente
|
Empieza con: tan(x) = sin(x) / cos(x) |
||
|
Luego agrega:
|
||
| Para ayudarte a recordar: todas las funciones "co" están a la derecha | ||
Bueno, ahora podemos seguir "todo el día" (en cualquier dirección) para obtener todas las "Identidades de cociente":
| En sentido horario |
|
| En sentido anti-horario |
|
Identidades Producto
El hexágono también muestra que una función entre dos funciones es igual a ellas dos multiplicadas (si están opuestas, entonces el "1" está entre ellas):
| Ejemplo: tan(x)cos(x) = sin(x) |
Ejemplo: tan(x)cot(x) = 1 |
Algunos ejemplos más:
- sin(x)csc(x) = 1
- tan(x)csc(x) = sec(x)
- sin(x)sec(x) = tan(x)
¡Pero espera, hay más!
También puedes obtener las "Identidades Recíprocas", yendo "a través del 1"
| Aquí puedes ver que sin(x) = 1 / csc(x) |
Aquí están todas:
- sin(x) = 1 / csc(x)
- cos(x) = 1 / sec(x)
- cot(x) = 1 / tan(x)
- csc(x) = 1 / sin(x)
- sec(x) = 1 / cos(x)
- tan(x) = 1 / cot(x)
¡El plus!
Y también tenemos estas:
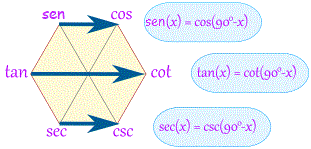
Ejemplos:
- sin(30°) = cos(60°)
- tan(80°) = cot(10°)
- sec(40°) = csc(50°)
¡Doble plus! Las identidades pitagóricas
El Círculo Unitario nos muestra que
sin2 x + cos2 x = 1
El hexágono mágico también puede ayudarnos a recordar eso, yendo en sentido horario alrededor de cualquiera de estos tres triángulos:
Y tenemos:
- sin2(x) + cos2(x) = 1
- 1 + cot2(x) = csc2(x)
- tan2(x) + 1 = sec2(x)
También puedes ir en sentido antihorario alrededor de un triángulo, por ejemplo:
- 1 - cos2(x) = sin2(x)
¡Espero que esto ayude!
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
