Bifurcación

Bifurcación significa dividirse en dos partes: "bi" (dos), y "furca" (tenedor).

¡Algunas funciones, al evolucionar, de repente se dividen en dos!

Primero necesitaremos una función:

rx(1−x) es una buena opción.

x es el valor de entrada, y r es un valor que queremos investigar.

Calcularemos la función una y otra vez, cada vez usando el resultado como el nuevo valor de x.

Probemos con r=2 y comenzamos con x=0.2:

2 × 0.2(1−0.2) = 2 × 0.2 × 0.8 = 0.32

Vemos que se está estabilizando en 0.5

Pero no siempre es tan simple. Prueba con otros valores de r aquí:

¿Qué notas?

• ¿Qué tal cuando r está alrededor de 3.2? Salta entre dos valores.
• Y alrededor de r = 3.5 salta entre cuatro valores.
• ¿Y qué ocurre alrededor de r = 3.7? Parece un completo caos.
• Pero luego, prueba alrededor de 3.84: se estabiliza brevemente y luego vuelve a enloquecer.

¡Necesitamos investigar más!

Prueba aquí. La misma idea que antes, pero un gráfico en la parte inferior sigue las últimas valores logrados para cada valor de r. Mueve el valor de r ya que necesita de tu ayuda para crear el gráfico:

Aquí tienes una mirada más cercana, nota las "bifurcaciones" (de donde proviene el nombre bifurcación), y también cómo pasa del orden al caos y a veces regresa al orden:

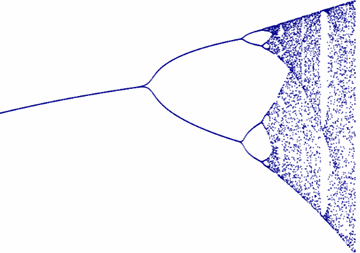
El cambio entre orden y caos también se observa en la naturaleza.

Por ejemplo, las poblaciones de animales pueden ser estables, mostrar un patrón de "un año muchos, otro año pocos", o simplemente ser muy caóticas.

Goteo de grifos

Haz que un grifo gotee.

Puede ser constante (goteo, goteo, goteo), pero a una velocidad de flujo diferente puedes obtener un "doble goteo" (como cuando r está alrededor de 3.2 para arriba).

Cambia el flujo nuevamente y los goteos pueden parecer aleatorios.

Como en estas fotos:

Conjunto de Mandelbrot

Hay una relación entre el diagrama de bifurcación y el conjunto de Mandelbrot. ¡Seguramente te interesará investigarlo!

Más

¡Hay más tipos de bifurcación en matemáticas!

Y hay mucho más por aprender en este tema realmente interesante llamado Sistemas Dinámicos.