Puertas Lógicas
Las puertas lógicas procesan valores de verdadero y falso.
Y (And*)
La puerta lógica "y" necesita que ambas entradas sean verdaderas para volverse verdadera.
Prueba a hacer clic en las líneas de la izquierda aquí (verde indica verdadero y azul falso):
*Frecuentemente se usa el nombre en inglés para las puertas lógicas, en este caso y es and.
Podemos mostrar eso en una "tabla de verdad" (V es para verdadero y F para falso):
| A | B | A y B | |
|---|---|---|---|
| F | F | F | |
| F | V | F | |
| V | F | F | |
| V | V | V |
Ejemplo: ¡Si cortamos el césped y lavamos el coche, obtenemos helado!
| cortar césped | lavar coche | helado | |
|---|---|---|---|
| F | F | F | |
| F | V | F | |
| V | F | F | |
| V | V | V |
Solo si hacemos ambos trabajos obtendremos helado.
O (Or)
La puerta lógica "o" puede tener cualquiera, o ambas, entradas verdaderas para volverse verdadera:
En una tabla de verdad:
| A | B | A o B | |
|---|---|---|---|
| F | F | F | |
| F | V | V | |
| V | F | V | |
| V | V | V |
Ejemplo: ¡Si cortamos el césped o lavamos el coche, obtenemos helado!
| cortar césped | lavar coche | helado | |
|---|---|---|---|
| F | F | F | |
| F | V | V | |
| V | F | V | |
| V | V | V |
En este caso, podemos hacer cualquiera de los trabajos (o ambos) para obtener helado. Vamos a lavar el coche.
Xor (O Exclusivo)
Xor es como o excepto que se vuelve falso cuando ambas entradas son verdaderas:
Aquí vemos o y xor en comparación una y otra:
| A | B | A o B | A xor B | |
|---|---|---|---|---|
| F | F | F | F | |
| F | V | V | V | |
| V | F | V | V | |
| V | V | V | F |
Xor es como si tus dos mejores amigos pelearan. La vida es divertida con cualquiera de los dos, pero no con ambos.
No
También podemos tener un "no" o "invertir":
- no verdadero es falso
- no falso es verdadero
Así queda en una "tabla de verdad":
| A |
no A | |
|---|---|---|
| F | V | |
| V | F |
Importante: es el círculo al final lo que lo convierte en "no":
Así que podemos indicar "no" en las otras puertas lógicas de la siguiente forma:
No y (Nand)
Nand es "y" con un "no", así que es verdadero excepto cuando ambas entradas son verdaderas:
Podemos mostrar eso en una "tabla de verdad" (V es para verdadero y F para falso):
| A | B | A y B | no (A y B) | |
|---|---|---|---|---|
| F | F | F | V | |
| F | V | F | V | |
| V | F | F | V | |
| V | V | V | F |
Nor
Nor es "o" con un "no", así que es verdadero solo si ninguna entrada es verdadera:
En una tabla de verdad:
| A | B | A o B | no (A o B) | |
|---|---|---|---|---|
| F | F | F | V | |
| F | V | V | F | |
| V | F | V | F | |
| V | V | V | F |
Xnor
Xnor es "xor" con un "no", así que es verdadero si ambas entradas son iguales (ambas falsas o ambas verdaderas):
En una tabla de verdad:
| A | B | A xnor B | |
|---|---|---|---|
| F | F | V | |
| F | V | F | |
| V | F | F | |
| V | V | V |
Ahora todo junto
Aquí están todos juntos:
| entrada |
salida | |||||||||
| A | B | y | no y (nand) | o | no o (nor) |
xor | xnor | |||
|---|---|---|---|---|---|---|---|---|---|---|
| F | F | F | V | F | V | F | V | |||
| F | V | F | V | V | F | V | F | |||
| V | F | F | V | V | F | V | F | |||
| V | V | V | F | V | F | F | V | |||
Mira todo aquí en acción (intenta hacer clic en el nombre o en la línea de salida):
En el mundo real
Este chip clásico tiene 4 puertas nand:

Su diagrama de circuito se ve así:
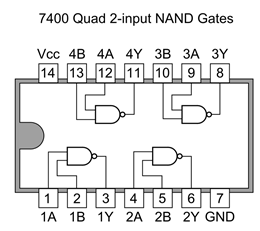
Ejemplo: puedes conectar los pines 1 y 2 a diferentes entradas, y obtendrás una salida del pin 3, excepto cuando ambos pines 1 y 2 estén encendidos.
(Nota: fuente de alimentación de 5 voltios entre "Vcc" y "GND")
Existen muchas variaciones de estos chips con diferentes puertas lógicas en su interior. Funcionan muy rápido (millones de veces por segundo), consumen muy poca energía y cuestan muy poco. Puedes combinarlos para hacer cosas sorprendentes.
