El Puzzle del Boxeador de Sam Loyd - Solución
Puzzles -> Puzzles de Sam Loyd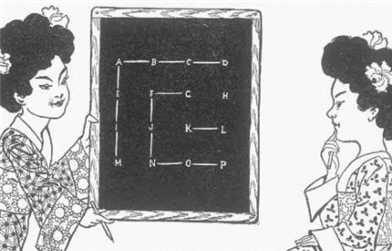 Puzzle: Aqui les vá un extraño pequeño puzzle desde el oriente:Una de las Niñas Chinas escribe dieciseis letras en una pizarra en cuatro filas, como se muestra, y luego de realizar una carrera recta, que conecta A con B, pasa la pizarra a su oponente quien conecta E con A. Si la primera jugadora deber ahora conectar E con F la otra jugadora conectaría B con F y anotaría "una caja", y tendría el derecho de jugar otra vez. Pero han jugado tan bién que nadie ha anotado "una caja", aunque cada una ha jugado seis veces, pero el juego está alcanzando un punto crítico en el cual una de ellas debe ganar, porque no existen los empates (porque hay nueve cajas en este juego) como en otros juegos. la pequeña joven sentada tiene que jugar ahora, y si ella conecta M con N su oponente anotaría cuatro cajas en una jugada, y entonces tendría el derecho de hacer un juego más y conecter H y L, lo que ganaría al resto. Que juego aconsejarías ahora,y cuantas cajas ganaría este juego an contra del mejor juego posible de la segunda jugadora? |
.
.
.
.
(Véase abajo si usted realmente desea
ver la solución ... )
.
.
.
.
.
.
La solución . . .
| Hay muchas posibles mejores jugadas. Una de las mejores jugadas es la siguiente: la primera jugadora anotaría 7 cajas empezando con una línes de G a H. Si la segunda jugadora luego marca de J a K, la primera anotará dos cajas marcando de K a O y P a L, y jugaría a, L a H, en vez de anotar dos cajas más. La otra jugadora ahora anota las dos cajas junto a G y K, y es entonces obligada a hacer una jugada que le dá a la primera 5 cajas más. Si, cuando la primera jugadora marca de G a H, la segunda jugadora marca C-G, B-F, E-F, y entonces le toca esperar jugando M-N, lo cual anota cuatro cajas más. Esta jugada astuta de darle al oponente dos cajas para obtener cuatro lo que constituye los puntos que ganan el juego. |
