Vectores
Este es un vector:
Un vector tiene magnitud (longitud) y dirección:
Juega con este vector:
Y no importa en qué orden los sumemos, obtenemos el mismo resultado:
Ejemplo: un avión está volando, apuntando hacia el norte, pero hay un viento que viene del noroeste.
Si observaras el avión desde el suelo, parecería que se desliza un poco hacia un lado.
¿Alguna vez has visto que eso suceda? Tal vez hayas visto pájaros luchando contra un fuerte viento que parecieran volar de lado. Los vectores ayudan a explicar eso.
La Velocidad, aceleración, fuerza y muchas otras cosas son vectores.
Restando
También podemos restar un vector de otro:- primero invertimos la dirección del vector que queremos restar,
- luego los sumamos como de costumbre:
a − b
Notación
Los vectores se suelen escribir en negritas, como a o b.
| Un vector también se puede escribir con las letras de sus extremos con una flecha encima, así: |
Operaciones
Ahora ... ¿cómo hacemos los cálculos?La forma más común es separar primero los vectores en partes x y y, así:
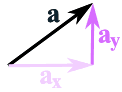
El vector a está separado
en dos vectores: ax y ay
(Veremos más adelante cómo hacer esto.)
Sumando vectores
Podemos sumar vectores sumando las partes x y sumando las partes y:
El vector (8, 13) y el vector (26, 7) se suman para formar el vector (34, 20)
Ejemplo: Sumar los vectores a = (8, 13) y b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
Cuando separamos un vector como ese, cada parte se llama componente:
Restando vectores
Para restar, primero invierte el vector que quieres restar, luego suma.
Ejemplo: Restar k = (4, 5) de v = (12, 2)
a = v + −k
a = (12, 2) + −(4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)
Magnitud de un vector
La magnitud de un vector se muestra mediante dos barras verticales a cada lado del vector:
|a|
O puede escribirse con barras verticales dobles (para no confundirlo con el valor absoluto):
||a||
Se usa el Teorema de Pitágoras para calcularla:
|a| = √( x2 + y2 )
Ejemplo: ¿Cuál es la magnitud del vector b = (6, 8)?
|b| = √( 62 + 82) = √( 36+64) = √100 = 10
Un vector con magnitud 1 se llama Vector Unitario.
Vector vs Escalar
Un escalar solamente tiene magnitud (tamaño).
Escalar: simplemente un número (como 7 o −0.32) ... definitivamente no es un vector.
- entonces c es un vector, tiene magnitud y dirección
- pero c es solo un valor, como 3 o 12.4
Ejemplo: kb es en realidad el escalar k veces el vector b.
Multiplicando un vector por un escalar
Cuando multiplicamos un vector por un escalar, se dice que "escalamos" un vector, porque estamos cambiando qué tan grande o pequeño es el vector.
Ejemplo: Multiplicar el vector m = (5, 2) por el escalar 3
|
a = 3(5,2) = (3×5,3×2) = (15,6) |
Todavía apunta en la misma dirección, pero es 3 veces más largo.
(Y ahora sabes porqué los números se llaman "escalares", porque "escalan" el vector hacia arriba o hacia abajo).
Multiplicar un Vector por un Vector (Producto Punto y Producto Cruz)
|
¿Cómo multiplicamos dos vectores entre sí? ¡Hay más de una forma!
(Lee esas páginas para más detalles). |
Más de 2 dimensiones
Los vectores también funcionan perfectamente bien en 3 o más dimensiones:
El vector (1, 4, 5)
Ejemplo: Sumar los vectores a = (3, 7, 4) y b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
Ejemplo: ¿Cuál es la magnitud del vector w = (1, −2, 3)?
|w| = √( 12 + (−2)2 + 32 ) = √( 1+4+9) = √14
Aquí hay un ejemplo con 4 dimensiones (¡pero es difícil de dibujar!):
Ejemplo: Restar (1, 2, 3, 4) de (3, 3, 3, 3)
(3, 3, 3, 3) + −(1, 2, 3, 4)
= (3, 3, 3, 3) + (−1,−2,−3,−4)
= (3−1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)
Magnitud y dirección
Podemos conocer la magnitud y dirección de un vector, pero querer sus longitudes x e y (o viceversa):
| <=> | ||
| Vector a en Coordenadas Polares |
Vector a en Coordenadas Cartesianas |
Puedes leer Coordenadas Polares y Cartesianas para saber cómo pasar de unas coordenadas a las otras, pero aquí te dejo un resumen:
| De coordenadas polares (r, θ) a coordenadas cartesianas (x,y) |
De coordenadas cartesianas (x, y) a coordenadas polares (r,θ) |
|
|---|---|---|
|
|
Un ejemplo
Samuel y Alex están tirando de una caja.
- Samuel jala con 200 Newtons de fuerza a 60°
- Alex jala con 120 Newtons de fuerza a 45°, como se muestra
¿Cuál es la fuerza combinada y su dirección?
Sumemos los dos vectores de extremo a origen:
Vector de Samuel:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sen( θ ) = 200 × sen(60°) = 200 × 0.8660 = 173.21
Vector de Alex:
- x = r × cos( θ ) = 120 × cos(−45°) = 120 × 0.7071 = 84.85
- y = r × sen( θ ) = 120 × sen(−45°) = 120 × -0.7071 = −84.85
Ahora tenemos:
Sumamos:
(100, 173.21) + (84.85, −84.85) = (184.85, 88.36)
Esa respuesta es válida, pero volvamos a polares ya que la pregunta era en polares:
- r = √ ( x2 + y2 ) = √ ( 184.852 + 88.362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88.36 / 184.85 ) = 25.5°
Y tenemos este resultado (redondeado):
Y se ve así para Samuel y Alex:
¡Podrían obtener un mejor resultado si estuvieran hombro con hombro!
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
