Producto Punto
Un vector tiene magnitud (qué tan largo es) y dirección:
Aquí hay dos vectores:
Se pueden multiplicar usando el "Producto Punto", también llamado Producto Escalar. (Ver también Producto Cruz).
Calcular
El Producto Punto se escribe utilizando un punto a media altura:
a · b
Esto indica el Producto Punto de a y b
Podemos calcular el Producto Punto de dos vectores de esta manera:
a · b = |a| × |b| × cos(θ)
Donde:
|a| es la magnitud (longitud) del vector a
|b| es la magnitud (longitud) del vector b
θ es el ángulo entre a y b
Entonces multiplicamos la longitud de a por la longitud de b, luego multiplicamos por el coseno del ángulo entre a y b.
O lo podemos calcular de esta manera:
a · b = ax × bx + ay × by
Entonces multiplicamos las x, multiplicamos las y, luego sumamos.
¡Ambos métodos funcionan!Y el resultado es un número (llamado "escalar", por lo que sabemos que no es un vector).
Ejemplo: calcular el producto escalar de vectores a y b:
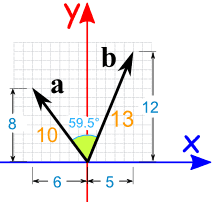
a · b = |a| × |b| × cos(θ)
O lo podemos calcular de esta manera:
a · b = ax × bx + ay × by
Ambos métodos obtuvieron el mismo resultado (después del redondeo)
También toma en cuenta que usamos menos 6 para ax (se dirige en la dirección negativa de x).
Nota: también puedes apoyarte usando la Calculadora
de Vectores.
¿Por qué cos(θ) ?
OK, para multiplicar dos vectores tiene sentido multiplicar sus longitudes juntas, pero solo cuando apuntan en la misma dirección.Entonces hacemos un "punto en la misma dirección" que el otro multiplicando por cos(θ):
| Tomamos el componente de a que se encuentra a lo largo de b |
Como si apuntáramos una luz para ver donde yace la sombra |
¡LUEGO multiplicamos!
| Funciona exactamente igual si "proyectamos" b a
lo largo de a y luego multiplicamos: Porque no importa en qué orden hacemos la multiplicación: |a| × |b| × cos(θ) = |a| × cos(θ) × |b| |
Ángulos rectos
Cuando dos vectores están en ángulo recto entre sí, el producto escalar es cero.
Ejemplo: calcular el producto punto para:
a · b = |a| × |b| × cos(θ)
O podemos calcularlo de esta manera:
a · b = ax × bx + ay × by
Esta puede ser una forma práctica de averiguar si dos vectores están en ángulo recto.
Tres o más dimensiones
Todo esto funciona bien en 3 (o más) dimensiones, también.¡Y en realidad puede ser muy útil!
Ejemplo: Samuel ha medido los puntos extremos de dos polos y quiere saber el ángulo entre ellos:
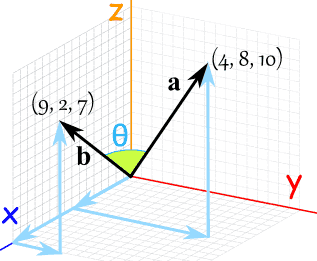
Tenemos 3 dimensiones, así que no olvides los componentes en z:
a · b = ax × bx + ay × by + az × bz
Ahora para la otra fórmula:
a · b = |a| × |b| × cos(θ)
¿ Pero qué es |a| ? Es la magnitud, o longitud, del vector a. Podemos usar Pitágoras:
- |a| = √(42 + 82 + 102)
- |a| = √(16 + 64 + 100)
- |a| = √180
Del mismo modo para |b|:
- |b| = √(92 + 22 + 72)
- |b| = √(81 + 4 + 49)
- |b| = √134
Y sabemos por el cálculo anterior que a · b = 122, así que:
a · b = |a| × |b| × cos(θ)
¡Listo!
Intenté un cálculo así una vez, pero trabajé todo en ángulos y distancias ... fue muy difícil, involucró mucha trigonometría y fue un dolor de cabeza. El método anterior es mucho más fácil.
Producto Cruz
El Producto Punto da un escalar (un número) como respuesta, y por ello a veces se le llama producto escalar, como se comentó más arriba en esta página.
Pero también está el Producto Cruz, que da como resultado un vector, por lo que también se conoce como producto vectorial.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
