Pendiente de una Función en un Punto
Utiliza este programa interactivo para encontrar la pendiente en un punto. Las instrucciones están más abajo.
Instrucciones
Escribe tu función en el recuadro superior ... tu función se grafica
en vivo.
Ahora arrastra los puntos "A" y "B" hacia la curva de la función.
Cuando estén cerca, se "ajustarán" a la función.
Lleva los puntos "A" y "B" cerca del punto donde deseas encontrar la
pendiente.
|
Cuando "A" y "B" están uno encima del otro, ¡la pendiente no
está definida! |
 |
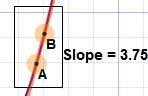 |
Haz un acercamiento: presiona "Ajustar". Y ahora puedes acercar los puntos nuevamente |
Sigue haciendo zoom y acercando los puntos hasta que estés
satisfecho con la respuesta.
¡Esta es la idea detrás del cálculo
diferencial! No podemos tener un espacio de cero (la
pendiente no estaría definida y podría ser cualquier cosa), pero
cuando el espacio se dirige hacia cero, la pendiente se dirige hacia
la pendiente verdadera en ese punto.
Funciones interesantes
Intenta encontrar la pendiente de y = x^2 en:
- x = 1
- x = 2
- x = 3
Intenta encontrar la pendiente de y = ln(x) en:
- x = 1
- x = 1.5
- x = 2
Intenta encontrar la pendiente de y = e^x en:
- y = 1 (x=0)
- y = 1.2
- y = 1.5
Exactitud
Hay solo unos pocos cientos de pixeles en cualquier dirección, por lo
que los cálculos no son totalmente precisos. Pero deberían darte una
buena idea de lo que está sucediendo.
Y no te preocupes, normalmente puedes utilizar el cálculo
diferencial para encontrar una respuesta exacta.
