Porcentaje de diferencia
Un porcentaje de diferencia es una diferencia dada como porcentaje.
¡Dos significados!
"Porcentaje de diferencia" quiere decir dos cosas, pero si estás comparando un valor antiguo con uno nuevo normalmente se usa este método:
Comparar antiguo y nuevo
Diferencia quiere decir restar un valor de otro. Por ejemplo la diferencia entre 5 y 3 es: 5−3 = 2. |
|
Porcentaje de diferencia quiere decir que se escribe la diferencia en forma de porcentaje del valor antiguo... así que divide entre el valor antiguo y conviértelo en porcentaje: Así que el porcentaje de diferencia entre 5 y 3 es: 2/5 = 0.4 = 40% |
Cómo se calcula
Hay dos maneras de calcular el porcentaje de diferencia, usa el que quieras:
Método 1
| Paso 1: calcula la diferencia (resta un valor del otro) |
| Paso 2: divide esa diferencia entre el valor antiguo (tendrás un número decimal) |
| Paso 3: convierte eso en un porcentaje (multiplícalo por 100 y añade un signo de "%") |
| Nota: si el valor nuevo es más grande que el antiguo, es un porcentaje de aumento, si no es de reducción. |
Método 2
| Paso 1: divide el valor nuevo entre el antiguo (tendrás un número decimal) |
| Paso 2: conviértelo en porcentaje (multiplicando por 100 y añadiendo un "%") |
| Paso 3: resta 100% a ese número |
| Nota: si el resultado es positivo es un porcentaje de aumento, si es negativo, sólo quítale el signo menos y llámalo una reducción. |
Ejemplos
Ejemplo: un par de calcetines pasó de costar $5 a $6, ¿cuál es el porcentaje de diferencia?
Respuesta (Método 1):
- Paso 1: de $5 a $6 es un aumento de $1
- Paso 2: divide entre el valor antiguo: $1/$5 = 0.2
- Paso 3: convierte 0.2 en porcentaje: 0.2×100 = aumento de 20%.
Respuesta (Método 2):
- Paso 1: divide el valor nuevo entre el anterior: $6/$5 = 1.2
- Paso 2: conviértelo en porcentaje: 1.2×100 = 120% (o sea, $6 es el 120% de $5)
- Paso 3: resta 100%: 120% − 100% = 20%, y eso quiere decir un aumento de 20%.
Otro ejemplo: había 160 chocolatinas en la caja ayer, pero ahora hay 116, ¿cuál es el porcentaje de diferencia?
 |
Respuesta (Método 1): de 160 a 116 es una reducción de 44. Comparado con el valor de ayer: 44/160 = 0.275 = reducción del 27.5%. |
| Respuesta (Método 2): compara el valor de hoy con el de ayer: 116/160 = 0.725 = 72.5%, así que el valor nuevo es el 72.5% del valor anterior. Resta 100% y tienes −27.5%, que es una reducción del 27.5%. |
La fórmula
También puedes poner los valores en esta fórmula:
|Valor nuevo - Valor anterior| |
× 100% |
|Valor anterior| |
(Los símbolos "|" quieren decir valor absoluto, así que los negativos se convierten en positivos)
Ejemplo: había 200 clientes ayer, y 240 hoy:
|240 − 200| |
× 100% = (40/200) × 100% = 20% |
|200| |
Un aumento de 20%.
Cómo se invierte un aumento o reducción
Alguna gente piensa que un porcentaje de aumento se puede "invertir" con el mismo porcentaje de reducción. ¡Pero no!
| Por ejemplo, un aumento del 10% de 100 es un aumento de 10, así que es 110 ... ... pero una reducción del 10% de 110 es una reducción de 11 (el 10% de 110 es 11), que es 99 (no el 100 con el que empezamos) |
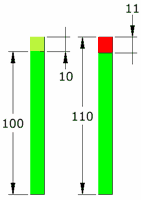 |
|
Esto pasa porque el porcentaje de aumento o reducción es en relación al valor antiguo:
|
Para "invertir" un porcentaje, usa la fórmula correcta:
| Para invertir: | Usa este porcentaje: | Ejemplo 10% |
|---|---|---|
| Un aumento de "x" por ciento: |
x/(1+x/100) |
10/(1+10/100) = 10/(1.1) = 9.0909... |
| Una reducción de "x" por ciento: |
x/(1−x/100) |
10/(1−10/100) = 10/(0.9) = 11.111... |
| O usa esta cómoda calculadora (sólo teclea un valor y pulsa en la otra caja) |

