Encontrar un Ángulo en un Triángulo Rectángulo
Un ángulo conociendo dos lados
Podemos encontrar un ángulo desconocido en un triángulo rectángulo, siempre que sepamos las longitudes de dos de sus lados.
Ejemplo
La escalera se apoya contra una pared como se muestra.¿Cuál es el ángulo entre la escalera y la pared?
¡La respuesta nos la da usar Seno, Coseno o Tangente!
Paso 1: Encuentra los nombres de los dos lados que conocemos
- Adyacente es el lado adyacente al ángulo,
- Opuesto es el lado opuesto al ángulo,
- y el lado más largo es la Hipotenusa.
Ejemplo: en nuestro ejemplo de escalera sabemos la longitud de:
- el lado Opuesto al ángulo "x", que mide 2.5
- el lado más largo llamado Hipotenusa, que mide 5
Paso 2: Ahora usa las primeras letras de esos dos lados (Opuesto e Hipotenusa) y la frase "SOHCAHTOA" para saber cuál usar: Seno, Coseno o Tangente:
Paso 3: Pon los valores en la ecuación Seno
Sen (x) = Opuesto / Hipotenusa = 2.5 / 5 = 0.5
Paso 4: ¡Ahora resuelve esa ecuación!
sen(x) = 0.5
A continuación (confía en mí por el momento) podemos reorganizar eso en esto:
x = sin-1(0.5)
Usa la calculadora, ingresa 0.5 y presiona el botón sin-1para obtener la respuesta:
x = 30°
Pero...¿Qué significa sin-1 … ?
Bueno, la función Seno "sin" toma un ángulo y nos da el cociente "opuesto/hipotenusa",
Pero sin-1 (llamado arcoseno o
seno inverso) va por el otro lado ...
... toma el cociente "opuesto/hipotenusa" y nos
da un ángulo.
Nota: Seno se representa como sen o sin. Esta
última abreviación viene del inglés sine.
Ejemplo:
- Función seno: sin(30°) = 0.5
- Función arcoseno: sin-1(0.5) = 30°
 |
En la calculadora presiona uno de las siguientes (dependiendo de la marca de calculadora): '2ndF sin' o 'shift sin'. |
¡En tu calculadora, intenta usar sin y sin-1 para ver qué resultados obtienes!
También intenta cos y cos-1.
Y tan y tan-1.
Vamos, pruébalo ahora.
Paso a Paso
Estos son los cuatro pasos que debemos seguir:
- Paso 1 Encontrar cuáles son los dos lados que conocemos – ya sean Opuesto, Adyacente o Hipotenusa.
- Paso 2 Decidir cuál usar: Seno, Coseno o Tangente.
- Paso 3 Para Seno calcular Opuesto/Hipotenusa, para Coseno calcular Adyacente/Hipotenusa o para Tangente calcular Opuesto/Adyacente.
- Paso 4 Encontrar el ángulo usando una calculadora. Utiliza sin-1, cos-1 o tan-1
Ejemplos
Veamos un par de ejemplos más:
Ejemplo
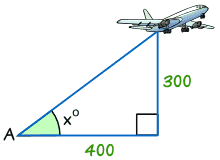
Encuentra el ángulo de elevación del plano desde el punto A en el suelo.
- Paso 1 Los dos lados que conocemos son Opuesto (300) y Adyacente (400).
- Paso 2 Debemos usar Tangente.
- Paso 3 Calculamos Opuesto/Adyacente = 300/400 = 0.75
- Paso 4 Encontramos el ángulo con la calculadora, usando tan-1
Tan x° = opuesto/adyacente = 300/400 = 0.75
tan-1 de 0.75 = 36.9° (correcto a 1 decimal)
A menos que se te indique lo contrario, los ángulos generalmente se redondean a un decimal.
Ejemplo
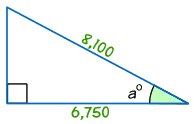
Encuentra el tamaño del ángulo a°
- Paso 1 Los dos lados que conocemos son Adyacente (6,750) e Hipotenusa (8,100).
- Paso 2 Debes usar Coseno.
- Paso 3 Calcula Adyacente/Hipotenusa = 6,750/8,100 = 0.8333
- Paso 4 Encuentra el ángulo con la calculadora, usando cos-1 de 0.8333:
cos a° = 6,750/8,100 = 0.8333
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
