Diferenciación Implícita
Encontrar la derivada cuando no puedes despejar y

Tal vez quieras leer primero Introducción a las Derivadas y Reglas de Derivación.
Implícita vs Explícita
Una función puede ser explícita o implícita:
Explícita: "y = alguna función de x". Cuando sabemos x podemos calcular y directamente.
Implícita: "alguna función de y y x es igual a otra cosa ". Saber x no conduce directamente a y.
Ejemplo: Un círculo
| Forma Explícita | Forma Implícita |
|
| y = ± √ (r2 − x2) | x2 + y2 = r2 | |
| De esta forma, y se expresa en función de x. |
De esta forma, la función es expresada en términos de y y x. |
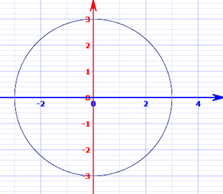
La gráfica
de x2 + y2 = 32
Cómo hacer Diferenciación Implícita
- Deriva con respecto a x
- Junta todos los dy dx de un lado
- Resuelve dy dx
Ejemplo: x2 + y2 = r2
Deriva con respecto a x:
d dx (x2) + d dx (y2) = d dx (r2)
Resolvamos cada término
Usa la Regla de la Cadena la Regla de la Cadena (se explica abajo): d dx (y2) = 2y dy dx
r2 es una constante, por lo que su derivada es 0: d dx (r2) = 0
Lo cual nos da:
2x + 2y dy dx = 0
Junta todos los dy dx de un solo lado
y dy dx = −x
Despeja dy dx :
dy dx = −x y
La Regla de la Cadena Usando dy dx
Veamos en detalle cómo d dx (y2) se convierte en 2y dy dx
La Regla de la Cadena dice:
du dx = du dy dy dx
Sustituye in u = y2:
d dx (y2) = d dy (y2) dy dx
Y luego:
d dx (y2) = 2y dy dx
Básicamente, todo lo que hicimos fue diferenciar con respecto a y y multiplicar por dy dx
Otra notación común es usar ’ para indicar d dx
La Regla de la Cadena Usando ’
La Regla de la Cadena también se puede escribir usando la notación ’ de esta forma:
f(g(x))’ = f’(g(x))g’(x)
g(x) es nuestra función "y", entonces:
f(y)’ = f’(y)y’
f(y) = y2, ergo f’(y) = 2y:
f(y)’ = 2yy’
o alternativamente: f(y)’ = 2y dy dx
Nuevamente, todo lo que hicimos fue diferenciar con respecto a y y multiplicar por dy dx
Explícita
Ahora encontremos también la derivada usando la forma explícita de la ecuación.
- Para resolver esto explícitamente, podemos despejar la ecuación para y
- Luego diferenciar
- Luego sustituir y nuevamente en la ecuación
Ejemplo: x2 + y2 = r2
Raíz cuadrada:y = ±√(r2 − x2)
Considera solo la parte positiva: y = √(r2 − x2)
Expresada como exponente: y = (r2 − x2)½
Derivada (Regla de la Cadena):y’ =½(r2 − x2)−½(−2x)
Simplifica:y’ = −x(r2 − x2)−½
Simplifica más:y’ = −x (r2 − x2)½
Ahora, considera y = (r2 − x2)½: y’ = −x/y
¡Obtenemos el mismo resultado de esta manera!
Puedes intentar tomar la derivada del término negativo tú mismo.
¡Otra vez la Regla de la Cadena!
Así es, en realidad usamos nuevamente la Regla de la Cadena. Así (considera que son letras diferentes, pero la regla es la misma):
dy dx = dy df df dx
Se sustituye en f = (r2 − x2):
d dx (f½) = d df (f½) d dx (r2 − x2)
Las derivadas:
d dx (f½) = ½(f−½) (−2x)
Se sustituye nuevamente f = (r2 − x2):
d dx (r2 − x2)½ = ½((r2 − x2)−½) (−2x)
Y simplificamos a partir de ahí.
Uso de la Derivada
Bien... ¿Para qué nos puede servir haber encontrado esta derivada y’ = −x/y ?
Bueno, por ejemplo, podemos encontrar la pendiente de una recta tangente.
Ejemplo: ¿Cuál es la pendiente de un círculo centrado en el origen con un radio de 5 en el punto (3,4)?
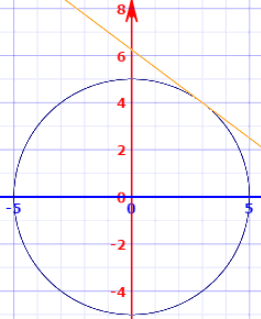
Sencillo, solo sustituye en nuestra ecuación:
dy dx = −x/y
dy dx = −3/4
Y como extra, la ecuación de la recta tangente es:
y = −3/4 x + 25/4
Otro Ejemplo
A veces, la forma implícita funciona cuando la forma explícita es difícil o imposible.
Ejemplo: 10x4 - 18xy2 + 10y3 = 48
¿Cómo despejamos y? ¡No tenemos que hacerlo!
- Primero, deriva con respecto a x (usa la regla del producto para el término xy2).
- Luego mueve todos los términos dy/dx al lado izquierdo.
- Resuelve dy/dx
*el término medio se explica más adelante
Y nos da:
Regla del Producto
Para el término medio usamos la regla del producto: (fg)’ = f g’ + f’ g
Porque (y2)’ = 2y dy dx (lo resolvimos en un ejemplo anterior).
Oh, y dxdx = 1, en otras palabras, x’ = 1
Funciones Inversas
La diferenciación implícita puede ayudarnos a resolver funciones
inversas.
El patrón general es:
- Empezar con la ecuación inversa en forma explícita. Ejemplo: y = sin−1(x)
- Reescribirla en modo no inverso: Ejemplo: x = sin(y)
- Diferenciar esta función con respecto a x en ambos lados.
- Resolver dy/dx
Como paso final podemos intentar simplificar más sustituyendo la
ecuación original.
Un ejemplo ayudará:
Ejemplo: la función seno inverso y = sin−1(x)
Empieza con:y = sin−1(x)
En modo no inverso:x = sin(y)
Deriva: d dx (x) = d dx sin(y)
1 = cos(y) dy dx
Pon dy dx a la izquierda: dy dx = 1 cos(y)
También podemos ir un paso más allá utilizando la identidad pitagórica:
sin2 y + cos2 y = 1
cos y = √(1 − sin2 y )
Y, como sin(y) = x (¡como se vio arriba!), obtenemos:
cos y = √(1 − x2)
Lo cual nos lleva a:
dy dx = 1 √(1 − x2)
Ejemplo: la derivada de la raíz de x, es decir, √x
Es decir:y2 = x
Deriva:2y dy dx = 1
Simplifica: dy dx = 1 2y
Dado que y = √x: dy dx = 1 2√x
Nota: esta es la misma respuesta que obtenemos usando la Regla de las Potencias:
Como potencia:y = x½
Regla de las Potencias d dx xn = nxn−1: dy dx = (½)x−½
Simplifica: dy dx = 1 2√x
Resumen
- Para derivar implícitamente una función (útil cuando una función
no se puede despejar fácilmente para y):
- Deriva con respecto a x
- Junta todos los dy dx de un lado
- Resuelve dy dx
- Para derivar una función inversa, reformúlala sin la parte inversa y luego usa la diferenciación implícita.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
