Intervalos
Intervalo: todos los números que están entre dos números dados.
Ejemplo: todos los números entre 1 y 6 son un intervalo
¿Todos los números?
Sí, todos los Números Reales que se encuentran entre esos 2 valores.
Ejemplo: el intervalo de 2 a 4 incluye números como:
¿Incluyendo los números en cada extremo?
Ahh ... tal vez sí, tal vez no ... ¡tenemos que decirlo!
Ejemplo: "Se permiten cajas de hasta 20 kg de masa"
Si tu caja pesa exactamente 20 kg ... ¿se
permitirá o no?
No es muy claro.
Veamos cómo ser precisos al respecto en cada uno de los tres métodos populares:
- Desigualdades
- La Recta Numérica
- Notación de Intervalos
Desigualdades
Con las desigualdades usamos:
- > mayor que
- ≥ mayor o igual que
- < menor que
- ≤ menor o igual que
Así:
Ejemplo: x ≤ 20
Nos indica: "x es menor o igual que 20"
Y significa: hasta 20 incluyendo el 20
Notación de Intervalos
En "Notación de Intervalos" simplemente escribimos los números inicial y final del intervalo y usamos:
- [ ] un corchete cuando queremos incluir el valor final, o
- ( ) un paréntesis cuando no lo incluimos
Así:
Ejemplo: (5, 12]
Significa de 5 a 12, y no incluye el 5, pero sí incluye el 12
Recta numérica
Con la recta numérica dibujamos una línea gruesa para mostrar los valores que estamos incluyendo, y:
- un círculo relleno cuando queremos incluir el valor final, o
- un círculo abierto cuando no lo incluimos
Así:
Ejemplo:
![(0, 20]](images/interval-0-20.gif)
nos indica todos los números entre 0 y 20, no se incluye al 0, pero sí se incluye el 20.
Los tres métodos juntos
Aquí hay una buena tabla que muestra los 3 métodos (el intervalo es de 1 a 2):
| de 1 | a 2 | ||||
| Incluyendo el 1 | No incluyendo al 1 | No incluyendo al 2 | Incluyendo el 2 | ||
| Desigualdad: | x ≥ 1 "mayor o igual que" |
x > 1 "mayor que" |
x < 2 "menor que" |
x ≤ 2 "menor o igual que" |
|
| Recta numérica: | 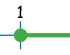 |
 |
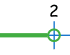 |
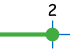 |
|
| Notación de intervalos: | [1 | (1 | 2) | 2] | |
Ejemplo: incluir el 1, y no incluir el 2:
| Desigualdad: |
x ≥ 1 y x < 2 o juntándolo: 1 ≤ x < 2 |
| Recta numérica: |   |
| Notación de intervalos: | [1, 2) |
Más ejemplos
Ejemplo 1: "La oferta: nada cuesta más de $10"
Eso significa hasta $10 inclusive.
Y es justo suponer que todos los precios son mayores a $ 0.00.
Como desigualdad mostramos esto como:
Precio ≤ 10 y Precio > 0
De hecho, podríamos combinar lo anterior así:
0 < Precio ≤ 10
En la recta numérica se ve así:
![(0, 10]](images/interval-0-10.gif)
Y usando la notación de intervalos es simplemente:
(0, 10]
Ejemplo 2: "Los competidores deben tener entre 14 y 18 años"
Así que los de 14 están incluidos, y "tener 18" va hasta, pero no incluye, 19 años (por ejemplo alguien puede tener 18 años y 364 días).Como desigualdad se ve así:
14 ≤ Edad < 19
En la recta numérica se ve así:
Y usando la notación de intervalos es simplemente:
[14, 19)
¿No es gracioso cómo medimos la edad de manera diferente a cualquier otra cosa? Nos quedamos en 18 hasta el momento en que cumplimos los 19. No decimos que tenemos 19 (redondeado al año más cercano) de 18½ en adelante.
Abierto o cerrado
Los términos "Abierto" y "Cerrado" a veces se utilizan cuando el valor final está incluido o no:
| (a, b) | a < x < b | un intervalo abierto | ||
| [a, b) | a ≤ x < b | cerrado a la izquierda, abierto a la derecha | ||
| (a, b] | a < x ≤ b | abierto a la izquierda, cerrado a la derecha | ||
| [a, b] | a ≤ x ≤ b | un intervalo cerrado |
Estos son intervalos de longitud finita. También tenemos intervalos de longitud infinita.
Al infinito (... ¡pero no más allá!)
A veces usamos al infinito en la notación de intervalos.
El infinito no es un número real, en este caso solo significa "continuar ..."
Ejemplo: x es mayor o igual que 3:
[3, +∞)
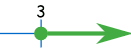
Ten en cuenta que usamos el corchete redondo con el infinito, ¡porque no lo alcanzamos!
Hay 4 posibles "extremos infinitos":
| Intervalo | Desigualdad | |||
| (a, +∞) | x > a | "mayor que a" | ||
| [a, +∞) | x ≥ a | "mayor o igual que a" | ||
| (-∞, a) | x < a | "menor que a" | ||
| (-∞, a] | x ≤ a | "menor o igual que a" |
Incluso podríamos mostrar ningún límite usando esta notación: (-∞, +∞)
Dos intervalos
Podemos tener dos (o más) intervalos.
Ejemplo: x ≤ 2 o x >3
En la recta numérica se ve así:
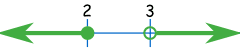
Y la notación de intervalos se ve así:
(-∞, 2] U (3, +∞)
Usamos una "U" para significar Unión (la unión de dos conjuntos).
|
Nota: ten cuidado con desigualdades como esa. 2 ≥ x > 3 eso no tiene sentido (no puedes ser menor que 2 |
Unión e intersección
Acabamos de ver cómo unir dos conjuntos usando "Unión" (y el símbolo ∪).
También hay "Intersección" que significa "tiene que estar en ambos". Piensa "¿dónde coinciden?".
El símbolo de intersección es una "U" invertida como esta: ∩
Ejemplo: (-∞, 6] ∩ (1, ∞)
El primer intervalo sube hasta (incluido) el 6
El segundo intervalo va desde (pero sin incluir) el 1 en adelante.
La intersección (o superposición) de esos dos conjuntos va de 1 a 6 (sin incluir el 1, incluido el 6):
(1, 6]
Conclusión
- Un intervalo son todos los números entre dos números dados.
- Indicar si se incluyen el número inicial y final es importante
- Hay tres formas principales de mostrar los intervalos: Desigualdades, La Recta Numérica y Notación de Intervalos.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
Nota al pie: geometría, álgebra y conjuntos
Puede que no hayas notado esto ... pero en realidad hemos estado usando:
- Álgebra,
- Geometría (la recta numérica es una línea), y
- Conjuntos (un intervalo es un conjunto de números)
Todo en un solo tema. ¿No son las matemáticas asombrosas?
 ¡error!
¡error!