Desviación Media
Cuán lejos, en promedio, están todos los valores del medio.
Cómo se calcula
Encuentra la media de todos los valores ... úsala para calcular distancias ... ¡luego encuentra la media de esas distancias!En tres pasos:
- 1. Encuentra la media de todos los valores
- 2. Encuentra la distancia de cada valor a la media (resta la media de cada valor, ignorando los signos negativos)
- 3. Luego encuentra la media de esas distancias
Así:
Ejemplo: la Desviación Media de 3, 6, 6, 7, 8, 11, 15, 16
Paso 1: Calcula la media:
Media = 3 + 6 + 6 + 7 + 8 + 11 + 15 + 168 = 728 = 9
Paso 2: Encuentra la distancia de cada valor a la media:
| Valor | Distancia al 9 |
|---|---|
| 3 | 6 |
| 6 | 3 |
| 6 | 3 |
| 7 | 2 |
| 8 | 1 |
| 11 | 2 |
| 15 | 6 |
| 16 | 7 |
Lo cual se ve así:
(¡Recuerda omitir los signos negativos!)
Paso 3. Encuentra la media de esas distancias:
Desviación Media = 6 + 3 + 3 + 2 + 1 + 2 + 6 + 78 = 308 = 3.75
Entonces, la media = 9, y la desviación media = 3.75
En ese ejemplo, los valores están, en promedio, a 3.75 del centro.
Para la desviación piensa en distancia.
Fórmula
La fórmula es:
Desviación Media = Σ|x − μ|N
- Σ es Sigma, que nos indica que hay que sumar
- || (las barras verticales) indican Valor Absoluto, básicamente ignorar signos negativos
- x es cada valor (como 3 o 16)
- μ es la media (en nuestro ejemplo μ = 9)
- N es la cantidad de valores (en nuestro ejemplo N = 8)
Veamos esto con más detalle:
Desviación Absoluta
Cada distancia que calculamos es una desviación absoluta, porque es el Valor Absoluto de la desviación (qué tan lejos de la media).
|
Para indicar "valor absoluto" ponemos las barras "|" de ambos lados, así: |-3| = 3 Para cualquier valor x: Desviación Absoluta = |x - μ| |
De nuestro ejemplo, el valor 16 tiene;
Desviación absoluta = |x - μ| = |16 - 9| = |7| = 7
Y ahora vamos a sumarlos todos ...
Sigma
El símbolo de "Sumar" es Σ (llamado Sigma), así que tenemos:
Suma de las Desviaciones Absolutas = Σ|x - μ|
Dividimos entre la cantidad de valores N y tenemos:
Desviación Media = Σ|x − μ| N
Hagamos nuestro ejemplo nuevamente, usando los símbolos apropiados:
Ejemplo: la Desviación Media de 3, 6, 6, 7, 8, 11, 15, 16
Paso 1: Encuentra la media
μ = 3 + 6 + 6 + 7 + 8 + 11 + 15 + 168 = 728 = 9
Paso 2: Encuentra las desviaciones absolutas:
| x | |x - μ| |
|---|---|
| 3 | 6 |
| 6 | 3 |
| 6 | 3 |
| 7 | 2 |
| 8 | 1 |
| 11 | 2 |
| 15 | 6 |
| 16 | 7 |
| Σ|x - μ| = 30 |
Paso 3. Encuentra la Desviación Media:
Desviación Media = Σ|x - μ|N = 308 = 3.75
Nota: la desviación media a veces se denomina desviación absoluta media (DAM) porque es la media de las desviaciones absolutas.
¿Y qué nos dice todo esto?
La Desviación Media nos dice qué tan lejos, en promedio, están todos
los valores de la media.
Aquí hay un ejemplo (usando los mismos datos que en
la página de Desviación Estándar):
Ejemplo: tú y tus amigos acaban de medir la altura de sus perros (en milímetros):
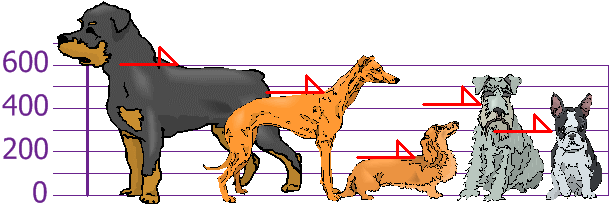
Las alturas (a los hombros) son: 600 mm, 470 mm, 170 mm, 430 mm y 300 mm.
Paso 1: Encuentra la media
μ = 600 + 470 + 170 + 430 + 3005 = 19705 = 394
Paso 2: Encuentra las desviaciones absolutas:
| x | |x - μ| |
|---|---|
| 600 | 206 |
| 470 | 76 |
| 170 | 224 |
| 430 | 36 |
| 300 | 94 |
| Σ|x - μ| = 636 |
Paso 3. Encuentra la Desviación Media:
Desviación Media = Σ|x - μ|N = 6365 = 127.2
Entonces, en promedio, las alturas de los perros están a 127.2 mm
de la media.
(Compara eso con la Desviación
Estándar de 147 mm)
Una comprobación útil
Las desviaciones en un lado de la media deben ser iguales a las desviaciones en el otro lado.De nuestro primer ejemplo:
Ejemplo: 3, 6, 6, 7, 8, 11, 15, 16
Las desviaciones son:
| 6 + 3 + 3 + 2 + 1 | = | 2 + 6 + 7 |
| 15 | = | 15 |
Del mismo modo:
Ejemplo: perros
Desviaciones a la izquierda de la media: 224 + 94 = 318
Desviaciones a la derecha de la media: 206 + 76 + 36 = 318
Si no son iguales ... ¡es posible que hayas cometido un errohr!
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
