Distancia Entre Dos Puntos

Explicación rápida

Triángulo rectángulo con lados a y b y la hipotenusa etiquetada como distancia

Cuando conocemos las distancias horizontal y vertical entre dos puntos, podemos calcular la distancia en línea recta así:

distancia = √ a2 + b2

Dos puntos etiquetados A y B en un plano cartesiano

Imagina que conocemos la ubicación de dos puntos (A y B) como aquí.

¿Cuál es la distancia entre ellos?

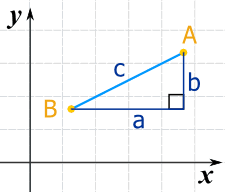
Puntos A y B conectados formando la hipotenusa de un triángulo rectángulo

Podemos trazar líneas hacia abajo desde A y líneas horizontales desde B para formar un triángulo rectángulo.

Y con un poco de ayuda de Pitágoras sabemos que:

a2 + b2 = c2

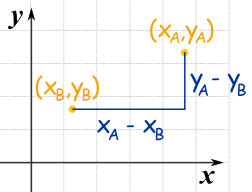
Triángulo rectángulo con lado horizontal xA menos xB y lado vertical yA menos yB

Ahora etiqueta las coordenadas de los puntos A y B.

xA significa la coordenada x del punto A
yA significa la coordenada y del punto A

La distancia horizontal a es (xA − xB)

La distancia vertical b es (yA − yB)

Ahora podemos resolver para c (la distancia entre los puntos):

Comienza con: c2 = a2 + b2 Sustituye los cálculos de a y b: c2 = (xA − xB)2 + (yA − yB)2 Raíz cuadrada en ambos lados: c = √(xA − xB)2 + (yA − yB)2
¡Listo! 

Ejemplos

Ejemplo 1

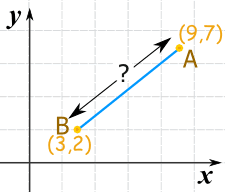
gráfica con 2 puntos

Sustituye los valores: c = √(9 − 3)2 + (7 − 2)2 Calcula: c = √62 + 52 c = √36 + 25
c = √61
c = 7.8102...

Ejemplo 2

No importa el orden en que estén los puntos. Una vez que elevamos al cuadrado el resultado, se vuelve positivo de todas formas:

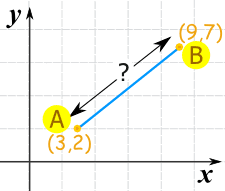
gráfica con 2 puntos

Sustituye los valores: c = √(3 − 9)2 + (2 − 7)2 Calcula: c = √(−6)2 + (−5)2 c = √36 + 25
c = √61
c = 7.8102...

Ejemplo 3

Y aquí hay otro ejemplo con algunas coordenadas negativas… y aun así todo funciona:

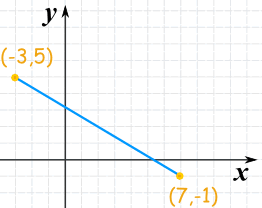
gráfica con 2 puntos

Sustituye los valores: c = √(−3 − 7)2 + (5 − (−1))2 Calcula: c = √(−10)2 + 62 c = √100 + 36
c = √136
c = 11.66...

(Nota: √136 se puede simplificar a 2√34 si se desea)

Inténtalo tú mismo

Arrastra los puntos:

images/dist2pts.js

Tres o más dimensiones

Funciona perfectamente en 3 (¡o más!) dimensiones.

Eleva al cuadrado la diferencia en cada eje, luego súmalas y toma la raíz cuadrada:

Distancia = √(xA − xB)2 + (yA − yB)2 + (zA − zB)2

Sistema de coordenadas 3D mostrando la distancia entre dos puntos

Ejemplo: la distancia entre los dos puntos (8,2,6) y (3,5,7) es:

  = √(8−3)2 + (2−5)2 + (6−7)2
  = √52 + (−3)2 + (−1)2
  = √25 + 9 + 1
  = √35

Lo cual es aproximadamente 5.9

Lee más en El Teorema de Pitágoras en 3D

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

 
Ecuación de una Recta con 2 Puntos Índice de Álgebra