Funciones pares e impares

Son tipos especiales de funciones

Funciones pares

Una función es "par" cuando:

f(x) = f(−x) para todo x

En otras palabras, hay simetría respecto al eje y (como una reflexión):

Esta es la curva f(x) = x²+1

Se llaman funciones "pares" porque las funciones x², x⁴, x⁶, x⁸, y así sucesivamente, se comportan así, pero también hay otras funciones que se comportan así, como cos(x):

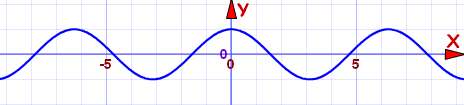
Función coseno: f(x) = cos(x)
Es una función par

Pero un exponente par no siempre hace una función par, por ejemplo (x+1)² no es una función par.

Funciones impares

Una función es "impar" cuando:

−f(x) = f(−x) para todo x

Observa el signo menos delante de f(x): −f(x).

Y se obtiene simetría respecto al origen:

Esta es la curva f(x) = x³−x

Se llaman "impares" porque las funciones x, x³, x⁵, x⁷, y así sucesivamente, se comportan así, pero también hay otras funciones que se comportan así, como sen(x):

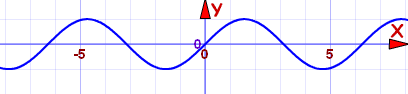
Función seno: f(x) = sen(x)
Es una función impar

Pero un exponente impar no siempre hace una función impar, por ejemplo x³+1 no es una función impar.

Ni par ni impar

No te dejes engañar por los nombres "par" e "impar" ... son solo nombres ... y una función no tiene que ser par o impar.

De hecho, la mayoría de las funciones no son ni impares ni pares. Por ejemplo, simplemente sumando 1 a la curva anterior se obtiene esto:

Esta es la curva f(x) = x³−x+1

No es una función impar, y tampoco es una función par.
No es ni par ni impar

¿Par o impar?

Par e impar

La única función que es par e impar es f(x) = 0

Propiedades especiales

Suma:

• La suma de dos funciones pares es par
• La suma de dos funciones impares es impar
• La suma de una función par y una impar no es par ni impar (a menos que una función sea cero)

Multiplicación:

• El producto de dos funciones pares es una función par
• El producto de dos funciones impares es una función par
• El producto de una función par y una función impar es una función impar

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).