Sucesiones Aritméticas y Sumas

Sucesión

Una Sucesión es un conjunto de cosas (generalmente números) que están en orden.

Sucesión

Cada número en la secuencia se llama término (o, a veces, "elemento" o "miembro"), lee Sucesiones y Series para más detalles.

Sucesión aritmética

En una sucesión aritmética, la diferencia entre un término y el siguiente es una constante.

En otras palabras, simplemente sumamos el mismo valor cada vez ... infinitamente.

Ejemplo:

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

Esta sucesión tiene una diferencia de 3 entre cada número.

El patrón continúa sumando 3 al último número cada vez, así:

sucesión aritmética 1,4,7,10,

En general, podríamos escribir una sucesión aritmética así:

{a, a+d, a+2d, a+3d, ... }

donde:

a es el primer término, y
d es la diferencia entre los términos (llamada "diferencia común")

Ejemplo: (continuación)

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

Tiene:

a = 1 (el primer término)
d = 3 (la "diferencia común" entre términos)

Y obtenemos:

{a, a+d, a+2d, a+3d, ... }

{1, 1+3, 1+2×3, 1+3×3, ... }

{1, 4, 7, 10, ... }

Regla

Podemos escribir una sucesión aritmética como regla:

x_n = a + d(n−1)

(Usamos "n−1" porque la d no se usa en el 1er término).

Ejemplo. Escribe una regla y calcula el noveno término para esta sucesión aritmética:

3, 8, 13, 18, 23, 28, 33, 38, ...

Esta sucesión tiene una diferencia de 5 entre cada número.

sucesión aritmética 3,8,13,18

Los valores de a y d son:

a = 3 (el primer término)
d = 5 (la "diferencia común")

Usando la regla de sucesión aritmética:

x_n = a + d(n−1)

= 3 + 5(n−1)

= 3 + 5n − 5

= 5n − 2

Entonces el noveno término es:

x₉ = 5×9 − 2
= 43

¿Está bien? ¡Compruébalo por ti mismo!

Las sucesiones aritméticas a veces se llaman progresiones aritméticas.

Tema avanzado: Sumar una serie aritmética

Para sumar los términos de esta sucesión aritmética:

a + (a+d) + (a+2d) + (a+3d) + ...

usa esta fórmula:

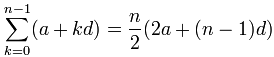
Sigma

¿Cuál es ese símbolo raro? Se llama Notación Sigma

(llamado Sigma) significa "suma"

Y abajo y arriba se muestran los valores iniciales y finales:

Notación Sigma

Dice "Suma n donde n va de 1 a 4. Respuesta=10

Aquí está cómo usarlo:

Ejemplo: Suma los primeros 10 términos de la sucesión aritmética:

{ 1, 4, 7, 10, 13, ... }

Los valores de a, d y n son:

a = 1 (el primer término)
d = 3 (la "diferencia común" entre términos)
n = 10 (la cantidad de términos a sumar)

Entonces:

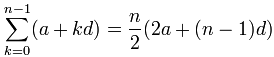
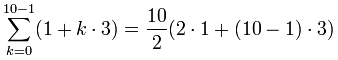
Sigma

Se convierte en:

Sigma

= 5(2+9·3) = 5(29) = 145

Verifica: ¿por qué no sumas los términos tú mismo y ves si realmente el resultado es 145?

Nota al pie: ¿Por qué funciona la fórmula?

Veamos porqué funciona la fórmula, pues podremos usar un "truco" interesante que vale la pena conocer.

Primero, llamaremos a toda la suma "S":

S = a + (a + d) + ... + (a + (n−2)d) + (a + (n−1)d)

Luego, reescribimos S en orden inverso:

S = (a + (n−1)d) + (a + (n−2)d) + ... + (a + d) + a

Ahora sumamos esas dos, término por término:

S	=	a	+	(a+d)	+	...	+	(a + (n-2)d)	+	(a + (n-1)d)
S	=	(a + (n-1)d)	+	(a + (n-2)d)	+	...	+	(a + d)	+	a

2S	=	(2a + (n-1)d)	+	(2a + (n-1)d)	+	...	+	(2a + (n-1)d)	+	(2a + (n-1)d)

¡Cada término es igual! Y hay "n" de ellos, así que ...

2S = n × (2a + (n−1)d)

Ahora, tan solo dividimos entre 2 y obtenemos:

S = (n/2) × (2a + (n−1)d)

Que es nuestra fórmula:

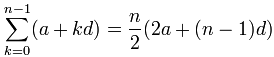
Sigma

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).