Sumas Parciales
Una Suma Parcial es una Suma de una Parte de una Sucesión.
Ejemplo:
Esta es la Sucesión de números pares de 2 en adelante: {2, 4, 6, 8, 10, 12, ...}
Esta es la Suma Parcial de los primeros 4 términos de esa sucesión: 2+4+6+8 = 20
Vamos a definir las cosas un poco mejor ahora:
Una Sucesión es un conjunto de cosas (generalmente números) que están en orden.
Una Suma Parcial es la suma de parte de la sucesión..
La suma de términos infinitos es una Serie Infinita.
Y las sumas parciales a veces se denominan "Series Finitas".
Sigma
Las sumas parciales a menudo se escriben usando Σ, queriendo decir "suma todo":
Así que Σ significa sumar cosas ...
¿Sumar qué? |
||
|
Suma lo que sea que esté después del Sigma: |
Σ
n
|
|
| así que sumamos n | ||
¿Pero qué valores de n? |
||
|
Los valores se muestran abajo. |
4
Σ
n=1
n
|
|
| dice que n va de 1 a 4, es decir, 1, 2, 3 y 4 |
||
OK, sígamos ... |
||
|
Entonces ahora sumamos 1, 2, 3 y 4: |
4
Σ
n=1
n = 1 + 2 + 3 + 4 = 10
|
|
Aquí está en un diagrama:
Más poder
¡Pero Σ
puede hacer cosas más poderosas que eso!
Podemos elevar n al cuadrado cada vez y sumar el resultado:
Podemos sumar los primeros cuatro términos en la sucesión 2n+1:
Y podemos usar otras letras, aquí usamos i y sumamos i × (i+1), yendo de 1 a 3:
Y podemos comenzar y terminar con cualquier número. Aquí vamos de 3 a 5:
Propiedades
Las Sumas Parciales tienen algunas propiedades útiles que pueden ayudarnos a hacer los cálculos.
Multiplicar por una Constante
Digamos que tenemos algo que queremos sumar, llamémoslo ak
ak podría ser k2, o k(k-7)+2, o ... cualquier cosa en realidad
Y c es un valor constante( como 2, ó -9.1, etc), entonces:
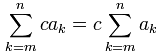
En otras palabras: si cada término que estamos sumando se multiplica por una constante, podemos "sacar" la constante fuera de la sigma.
Ejemplo:
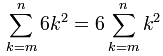
De modo que en lugar de sumar 6k2 podemos sumar k2 y luego multiplicar el resultado por 6
Sumar o Restar
Aquí hay otra propiedad útil:
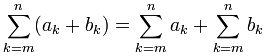
Lo que significa que cuando se suman dos términos y queremos sumarlos dentro de un Sigma, en realidad podemos sumarlos por separado y luego sumar los resultados.
Ejemplo:
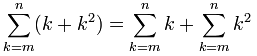
Será más fácil hacer las dos sumas y luego sumarlas al final.
Ten en cuenta que esto también funciona para la resta:
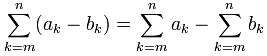
Atajos útiles
Y aquí hay algunos atajos útiles que hacen que las sumas sean mucho más fáciles.En cada caso estamos tratando de sumar de 1 a algún valor n.
| Sumar 1 es igual a n | ||
| Sumar la constante c es igual a c veces n | ||
| Un atajo a la hora de sumar k | ||
| Un atajo a la hora de sumar k2 | ||
| Un atajo a la hora de sumar k3 | ||
| Otra alternativa para sumar k3 | ||
| Suma de números impares |
Usemos algunos de esos:
Ejemplo 1: Vendes ladrillos para paisajismo.
Un cliente dice que comprará la "pirámide" completa de ladrillos que
tienes al frente de tu tienda. La pila tiene 14 ladrillos de altura.
¿Cuántos ladrillos hay ahí?
Cada capa es un cuadrado, por lo que el cálculo que tenemos que hacer es:
12 + 22 + 32 + ... + 142
Pero esto se puede escribir mucho más fácilmente como:
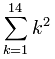
Podemos usar la fórmula para k2 de arriba:
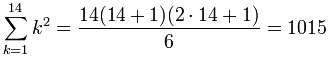
Eso fue mucho más fácil que sumar 12 + 22 + 32 + ... + 142.
Y aquí hay un ejemplo más complicado:
Ejemplo 2: El cliente quiere un mejor precio.
El cliente dice que los ladrillos en el exterior de la pirámide deberían ser más baratos, ya que necesitan limpieza.Tú aceptas y propones:
- $7 por ladrillos exteriores
- y $11 por ladrillos interiores.
Puedes calcular cuántos bloques "internos" y "externos" en cualquier capa (excepto la primera) usando
- ladrillos exteriores = 4×(tamaño-1)
- ladrillos interiores = (tamaño-2)2
Y entonces el costo por capa es:
- costo (ladrillos exteriores) = $7 × 4(tamaño-1)
- costo (ladrillos interiores) = $11 × (tamaño-2)2
Entonces, todas las capas juntas (excepto la primera) costarán:
![Sigma [7*4(i-1) + 11*(i-2)^2]](images/partial-sum-ex2-b.gif)
Usando la "Propiedad de Suma" de arriba:
![Sigma [7*4(i-1)] + Sigma [11*(i-2)^2]](images/partial-sum-ex2-c.gif)
Usando la "Propiedad de Multiplicación por una Constante" de arriba:
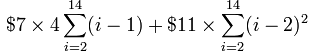
Eso es bueno ... pero no podemos usar ningún atajo como está, ya que vamos desde i=2 en lugar de i=1
SIN EMBARGO, si inventamos dos nuevas variables:
- j = i-1
- k = i-2
Tenemos:
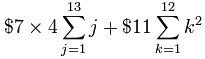
(Dejé de lado el caso k = 0, porque sé que 02=0)
Y ahora podemos usar los atajos:
![]()
Después de un pequeño cálculo:
$7 × 364 + $11 × 650 = $9,698.00
¡Oh! Y no olvides la capa superior (tamaño = 1) que es solo un ladrillo. Tal vez puedas dar ese gratis, ¡eres tan generoso!Nota: como comprobación, cuando sumamos los ladrillos "externo" e "interno", más el que está arriba, obtenemos
364 + 650 + 1 = 1015
El cual es el mismo número que obtuvimos para los "ladrillos totales" antes ... ¡Súper!
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
