Series Infinitas
La suma de términos infinitos que siguen una regla.
Cuando tenemos una secuencia infinita de valores:
12 , 14 , 18 , 116 , ...
que siguen una regla (en este caso, cada término es la mitad del anterior),
y los sumamos todos:
12 + 14 + 18 + 116 + ... = S
obtenemos una serie infinita.
"Serie" suena como si fuera la lista de números, pero en realidad es cuando los sumamos.
(Nota: los puntos "..." significan "continuar indefinidamente")
Primer ejemplo
Puedes pensar que es imposible encontrar la respuesta, ¡pero a veces se puede hacer!Usando el ejemplo de arriba:
12 + 14 + 18 + 116 + ... = 1
Y aquí está el porqué:
(También mostramos una prueba usando Álgebra a continuación)
Notación
A menudo se usa la Notación Sigma para series infinitas. Nuestro ejemplo de arriba se ve así:
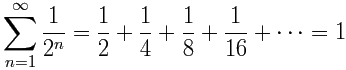
| Este símbolo (llamado Sigma) significa "sumar" |
Intenta poner 1/2^n en la Calculadora Sigma.
Otro ejemplo
14 + 116 + 164 + 1256 + ... = 13
Cada término es un cuarto del anterior, y la suma es igual a 1/3:
De los 3 espacios (1, 2 y 3) solo se llena el número 2, por lo tanto,
1/3.
(Por cierto, éste fue resuelto por Arquímedes hace más de 2200 años).
Convergencia
Sumemos los términos uno a la vez. Cuando la "suma hasta un cierto valor" se acerca a un valor finito, se dice que la serie es "convergente":
Nuestro primer ejemplo:
12 + 14 + 18 + 116 + ...
Va sumando así:
| Término | Suma hasta cierto valor | |
| 1/2 | 0.5 | |
| 1/4 | 0.75 | |
| 1/8 | 0.875 | |
| 1/16 | 0.9375 | |
| 1/32 | 0.96875 | |
| ... | ... |
Las sumas se dirigen hacia un valor (1 en este caso), por lo que esta serie es convergente.
La "suma hasta cierto valor" se llama sumas parcial .
Entonces, más formalmente, decimos que es una serie convergente cuando:
"la secuencia de sumas parciales tiene un límite finito".
Divergencia
Si las sumas no convergen, se dice que la serie diverge.Puede ir a +infinito, −infinito o simplemente subir y bajar sin establecer ningún valor.
Ejemplo:
1 + 2 + 3 + 4 + ...
Va sumando así:
| Término | Suma hasta cierto valor |
|
| 1 | 1 | |
| 2 | 3 | |
| 3 | 6 | |
| 4 | 10 | |
| 5 | 15 | |
| ... | ... |
No converge, por lo que es divergente y se dirige al infinito.
Ejemplo: 1 − 1 + 1 − 1 + 1 ...
Sube y baja sin establecerse en algún valor, por lo que es divergente.
Más ejemplos
Series Aritméticas
Cuando la diferencia entre cada término y el siguiente es una constante, se llama una serie aritmética.
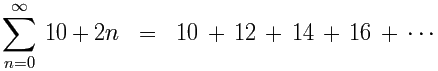
(La diferencia entre cada término es 2).
Series Geométricas
Cuando la razón entre cada término y el siguiente es una constante, se llama una serie geométrica.Nuestro primer ejemplo de arriba es una serie geométrica:
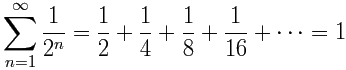
(La razón entre cada término es ½)
Y, como se prometió, podemos mostrarte porqué esa serie es igual a 1 usando Álgebra:
Ahora restamos S/2 de S
Todos los términos de 1/4 en adelante se cancelan.
Serie armónica
Ésta es la serie armónica:
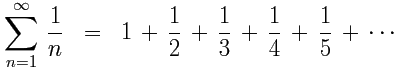
Es divergente.
¿Cómo lo sabemos? Comparémosla con otra serie:
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + ... | ||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||||
| etc... | |||||||||||||||||||
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + ... | ||
| 2 | 4 | 4 | 8 | 8 | 8 | 8 | 16 | ||||||||||||
En cada caso, los valores superiores son iguales o mayores que los valores inferiores.
Ahora, sumemos los grupos inferiores:
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | ... | + ... | ||
| 2 | 4 | 4 | 8 | 8 | 8 | 8 | 16 | |||||||||||||
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + ... = ∞ | |||||||||||
| 2 | 2 | 2 | 2 | |||||||||||||||||
Esa serie es divergente.
Entonces la serie armónica también debe ser divergente.
Aquí hay otra forma:
Podemos dibujar el área de cada término y compararlo con el área bajo la curva 1/x:
1/x vs el área de la serie armónica
El cálculo nos dice que el área bajo 1/x (de 1 en adelante) se aproxima a infinito, y la serie armónica es mayor que eso, por lo que debe ser divergente.
Series alternantes
Una serie alternante tiene términos que alternan entre positivo y negativo.Puede o no converger.
Ejemplo: 12 − 14 + 18 − 116 + ... = 13
Esta ilustración puede convencerlo de que los elementos convergen en 13:
¿Quizás puedas probarlo tú mismo? Intenta emparejar cada par positivo y negativo, luego busca arriba una serie que coincida.
Otro ejemplo de una serie alternante (basada en la serie armónica anterior):
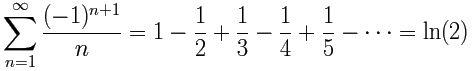
Ésta converge en el logaritmo natural de 2
Explicación avanzada:
Para mostrar PORQUÉ, primero comenzamos con un cuadrado del área 1, y luego emparejamos las fracciones menos y más para mostrar cómo reducen el área al área debajo de la curva y=1/x entre 1 y 2:
¿Puedes ver que lo que queda es el área de 1/x de 1 a 2?
Usando cálculo integral (por ahora confía) ésa área es ln(2):
¡Tú puedes investigar esto en más detalle!
- ¿Realmente esos rectángulos forman el área sobre la curva como se muestra?
- ¿El área debajo de la curva es realmente ln(2) = 0.693 ...? Prueba la Calculadora de Aproximación de Integrales para comprobarlo (y=1/x entre 1 y 2)
¡Orden!
¡El orden de los términos puede ser muy importante! A veces podemos obtener resultados extraños cuando cambiamos su orden.Por ejemplo, en una serie alternante, ¿qué pasa si hacemos que todos los términos positivos sean los primeros? ¡Así que ten cuidado!
Más
Existen otros tipos de series infinitas, y es interesante (¡y a menudo desafiante!) determinar si son convergentes o no, y a qué pueden converger.
