Identidades Trigonométricas
¡Tal vez quieras leer sobre Trigonometría primero!
Triángulo rectángulo
Las Identidades Trigonométricas son ecuaciones que son verdaderas para Triángulos Rectángulos. (Si no se trata de triángulos rectángulos, revisa la página de Identidades de Triángulos).
Cada lado de un triángulo rectángulo tiene un nombre:
Adyacente es el que está al lado del ángulo
Y Opuesto es el opuesto al ángulo
Pronto vamos a jugar con todo tipo de funciones, pero recuerda que todo siempre regresa a ese simple triángulo con:
- Ángulo θ
- Hipotenusa
- Adyacente
- Opuesto
Seno, coseno y tangente
Las funciones principales en trigonometría son Seno, Coseno y Tangente
Estas funciones son simplemente un lado de un triángulo rectángulo dividido por otro.
Para un triángulo rectángulo con un ángulo "θ":
|
Función Seno:
|
sin(θ) = Opuesto / Hipotenusa |
|
Función Coseno:
|
cos(θ) = Adyacente / Hipotenusa |
|
Función Tangente:
|
tan(θ) = Opuesto / Adyacente |
Para un ángulo dado θ cada
relación permanece igual
no importa cuán grande o pequeño sea el triángulo
Nota: recuerda que Seno tiene dos abreviaciones en español: sen y sin.
Cuando dividimos seno por coseno obtenemos:
sin(θ)cos(θ) = Opuesto/HipotenusaAdyacente/Hipotenusa = OpuestoAdyacente = tan(θ)
Así que podemos decir:
tan(θ) = sin(θ)cos(θ)
Esa es nuestra primera Identidad Trigonométrica.
Cosecante, secante y cotangente
También podemos dividir "al revés" (como Adyacente/Opuesto en vez de Opuesto/Adyacente):
|
Función Cosecante:
|
csc(θ) = Hipotenusa / Opuesto |
|
Función Secante:
|
sec(θ) = Hipotenusa / Adyacente |
|
Función Cotangente:
|
cot(θ) = Adyacente / Opuesto |
Ejemplo: cuando Opuesto=2 e Hipotenusa=4 entonces
sin(θ) = 2/4, y csc(θ) = 4/2
Por todo lo anterior podemos decir:
sin(θ) = 1/csc(θ)
cos(θ) = 1/sec(θ)
tan(θ) = 1/cot(θ)
Y a la inversa:
csc(θ) = 1/sin(θ)
sec(θ) = 1/cos(θ)
cot(θ) = 1/tan(θ)
Y también tenemos:
cot(θ) = cos(θ)/sin(θ)
Teorema de Pitágoras
Para las próximas identidades trigonométricas comenzamos con el Teorema de Pitágoras:
 |
El Teorema de Pitágoras dice que, en un triángulo rectángulo, el cuadrado de a más el cuadrado de b es igual al cuadrado de c: a2 + b2 = c2 |
Si dividimos todo por c2 tenemos
a2 c2 + b2 c2 = c2 c2
Lo cual se puede simplificar a esto:
( a c )2 + ( b c )2 = 1
Ahora, a/c es Opuesto/Hipotenusa, lo que es sin(θ)
Y b/c es Adyacente/Hipotenusa, lo que es cos(θ)
Así que (a/c)2 + (b/c)2 = 1 también se puede escribir así:
sin2 θ + cos2 θ = 1
- sin2 θ significa encontrar el seno de θ, luego elevar al cuadrado el resultado y
- sin θ2 significa elevar al cuadrado θ, luego aplicar la función seno
Ejemplo: 32°
Usando solo 4 decimales:
- sin(32°) = 0.5299...
- cos(32°) = 0.8480...
Ahora, calculemos sin2 θ + cos2 θ:
0.52992 + 0.84802
= 0.2808... + 0.7191...
= 0.9999...
Nos acercamos mucho a 1 usando solo 4 decimales. Pruébalo en tu calculadora, ¡podrías obtener mejores resultados!
Las identidades relacionadas incluyen:
sin2 θ = 1 − cos2 θ
cos2 θ = 1 − sin2 θ
tan2 θ + 1 = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
¿Cómo se pueden recordar?Las identidades mencionadas hasta ahora pueden recordarse
|
 |
¡Pero espera... Hay más!
Hay muchas más identidades ... aquí están algunas de las más útiles:
Identidades del Ángulo Negativo
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
Identidades del Ángulo Doble
![sin 2a = 2tan(a)/[1+tan^2(a)]](images/trig-sin2theta.gif) |
 |
 |
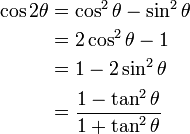Identidades de la Mitad del Ángulo
Observa que "±" significa que puede ser cualquiera de las dos, dependiendo del valor de θ/2
 |
 |
 |
 |
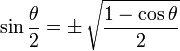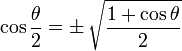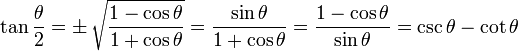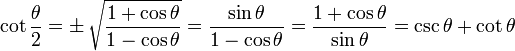Identidades de Suma y Resta de Ángulos
Observa que 
significa que puedes usar más o menos, y el 
significa que debes usar el signo opuesto.
sin(A
B) = sin(A)cos(B)
cos(A)sin(B)
cos(A
B) = cos(A)cos(B)
sin(A)sin(B)
tan(A
B) = tan(A) tan(B)1 tan(A)tan(B)
cot(A
B) = cot(A)cot(B) 1cot(B) cot(A)
Identidades de triángulos
También hay Identidades de Triángulos que se aplican a todos los triángulos (no solo a los triángulos rectángulos).
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
