Seno, coseno y tangente
Triángulo rectángulo
Seno, Coseno y Tangente son las tres funciones principales que se usan en Trigonometría y están basadas en un triángulo rectángulo.
Antes de concentrarnos en las funciones, nos ayudará dar nombres a los lados de un triángulo rectángulo, de esta manera:

- "Opuesto" es opuesto al ángulo θ
- "Adyacente" es adyacente (al lado de) al ángulo θ
- "Hipotenusa" es el lado más largo
El Adyacente siempre está al lado del ángulo
Y el Opuesto está opuesto al ángulo
Seno, Coseno y Tangente
Seno, Coseno y Tangente (a menudo abreviadas como sen -o sin, del inglés sine-, cos y tan) son cada una una proporción de los lados de un triángulo rectángulo:
Para un ángulo dado θ cada
proporción permanece igual
no importa cuán grande o pequeño sea el triángulo
Para calcularlas:
Divide la longitud de un lado por otro lado.
Ejemplo: ¿Cuál es el seno de 35°?
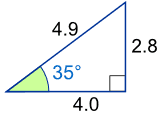
Usando este triángulo (las longitudes están redondeadas a un decimal):
| sin(35°) | = OpuestoHipotenusa |
| = 2.84.9 | |
| = 0.57... | |
| cos(35°) | = AdyacenteHipotenusa |
| = 4.04.9 | |
| = 0.82... | |
| tan(35°) | = OpuestoAdyacente |
| = 2.84.0 | |
| = 0.70... |
El tamaño no importa
El triángulo puede ser grande o pequeño y la razón de los
lados permanece igual.
Solo el ángulo cambia la proporción.
Intenta arrastrar el punto "A" para cambiar el ángulo y el punto "B"
para cambiar el tamaño:

Las buenas calculadoras incluyen sin, cos y tan. Simplemente pones el
ángulo y presionas el botón.
¡Pero aún necesitas recordar lo que significan!
Las tres funciones ilustradas individualmente:
Practica aquí:
Sohcahtoa
¿Cómo puedes recordar todo esto? ¡Piensa "Sohcahtoa"!
Funciona así:
|
Soh...
|
Seno = Opuesto / Hipotenusa
|
|
...cah...
|
Coseno = Adyacente / Hipotenusa
|
|
...toa
|
Tangente = Opuesto / Adyacente
|
Tenemos una página sobre esta mnemotecnia sohcahtoa ... ¡te puede ayudar en un examen!
Ángulos de 0° a 360°
Mueve el cursor para ver cómo los diferentes ángulos (en radianes o grados) afectan los valores de seno, coseno y tangente.
En esta animación, la hipotenusa es 1, formando una circunferencia unitaria.
Observa que el lado adyacente y el lado opuesto pueden ser positivos o negativos, lo que hace que el seno, el coseno y la tangente también cambien entre valores positivos y negativos.
no llegaron a su destino?" Porque se salieron por la tangente. |
Ejemplos
Ejemplo: ¿cuáles son los valores del seno, coseno y la tangente de 30° ?
El clásico triángulo de 30° tiene una hipotenusa de longitud 2, un
lado opuesto de longitud 1 y un lado adyacente que mide √3:
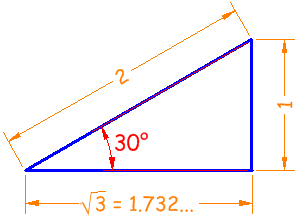
Ahora que conocemos las longitudes, podemos calcular las funciones:
|
Seno
|
sin(30°) = 1 / 2 = 0.5 | |
|
Coseno
|
cos(30°) = 1.732 / 2 = 0.866... | |
|
Tangente
|
tan(30°) = 1 / 1.732 = 0.577... |
(Ten a la mano tu calculadora y comprueba).
Ejemplo: ¿cuáles son los valores del seno, coseno y la tangente de 45° ?
El clásico triángulo de 45° tiene dos lados de longitud 1 y una
hipotenusa de √2:
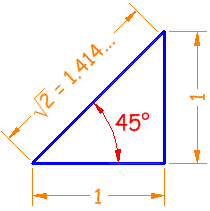
|
Seno
|
sin(45°) = 1 / 1.414 = 0.707... | |
|
Coseno
|
cos(45°) = 1 / 1.414 = 0.707... | |
|
Tangente
|
tan(45°) = 1 / 1 = 1 |
¿Por qué?
¿Por qué son importantes estas funciones?- Porque nos permiten conocer los ángulos cuando conocemos los lados
- Y nos permiten conocer los lados cuando conocemos los ángulos
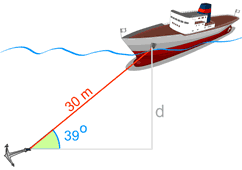
Ejemplo: Usa la función seno para encontrar "p"
Tenemos estos datos:
- El cable forma un ángulo de 39° con el
fondo del mar
- El cable tiene una longitud de 30 metros.
Y queremos saber "p" (la profundidad).
La profundidad "p" es 18.88 m
Ejercicio
Prueba este ejercicio sobre el papel donde tienes que calcular la función seno para ángulos de 0° a 360°, y dibujar el resultado. Te ayudará a entender estas funciones que son bastante simples.
También puedes leer acerca de las Gráficas de Seno, Coseno y Tangente.
Y jugar con un resorte que hace una onda sinusoidal (seno).
Funciones menos comunes
Para completar el cuadro, hay otras 3 funciones donde divides un lado por otro, pero no se usan tanto.
Son iguales a 1 dividido entre cos, 1 dividido entre sin y 1 dividido entre tan:
|
Función secante:
|
sec(θ) = HipotenusaAdyacente | (=1/cos) | ||
|
Función cosecante:
|
csc(θ) = HipotenusaOpuesto | (=1/sin) | ||
|
Función cotangente:
|
cot(θ) = AdyacenteOpuesto | (=1/tan) |
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).



