Circunferencia Unitaria
La "circunferencia unitaria" es simplemente una circunferencia de radio 1.
Como es tan simple, es perfecta para aprender a hablar de longitudes y ángulos.
El centro se pone donde se cruzan el eje x y el eje y, así que nos queda este dibujo tan sencillo.
Seno, coseno y tangente
Como el radio es 1, puedes medir directamente el seno, el coseno y la tangente.
¿Qué pasa cuando el ángulo θ es 0°?
cos 0° = 1, sin 0° = 0 y tan 0° = 0
¿Qué pasa cuando θ es 90°?
cos 90° = 0, sin 90° = 1 y tan 90° no está definida
¡Prueba tú!
¡Inténtalo tú ahora! Arrastra la esquina alrededor de la circunferencia para ver los distintos ángulos (en radianes o grados) y cómo cambian el seno, coseno y tangente.
¿Puedes encontrar un ángulo donde el seno y el coseno sean iguales?
Fíjate en que los "lados" pueden ser positivos o negativos según las reglas de las coordenadas cartesianas. Esto hace que el seno, coseno y tangente también vayan alternando entre positivo y negativo.
También prueba la Circunferencia Unitaria Interactiva.
Pitágoras
El teorema de Pitágoras dice que en un triángulo rectángulo, el cuadrado del lado largo es igual a la suma de los cuadrados de los otros dos lados:
x2 + y2 = 12
Pero 12 es 1, así que:
x2 + y2
= 1
(la ecuación de la circunferencia unitaria)
Además, como x=cos e y=sen, tenemos:
(cos(θ))2 + (sen(θ))2 = 1
una "identidad" bastante útil
Ángulos relevantes: 30°, 45° y 60°
Debes intentar memorizar sen, cos y tan para los ángulos de 30°, 45° y 60°.Sí, sí, es un fastidio tener que recordar cosas, pero te hará la vida más fácil cuando los reconozcas, no solo en los exámenes, sino en otras ocasiones en las que necesites hacer estimaciones rápidas, etc.
¡Estos son los valores que debes recordar!
| Ángulo | Cos | Sen | Tan=Sen/Cos |
|---|---|---|---|
| 30° | √32 | 12 | 1 √3 = √3 3 |
| 45° | √22 | √22 | 1 |
| 60° | 12 | √32 | √3 |
Ayudándote a recordar
Para que te sea fácil recordar, el seno va "1,2,3" :
sen(30°) = √12 = 12 (porque √1 = 1)
sen(45°) = √22
sen(60°) = √32
Y el coseno va "3,2,1"
cos(30°) = √32
cos(45°) = √22
cos(60°) = √12 = 12
Solo 3 números
De hecho, saber 3 números es suficiente: 12 , √22 y √32
Porque funcionan para cos y sin:
Tu mano puede ayudarte a recordar:
Por ejemplo, hay 3 dedos por encima de 30°, por lo que cos(30°) = √32
¿Qué hay de la tangente?
Bueno, tan = sen/cos, para que podamos calcularla así:
tan(30°) =sen(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sen(45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sen(60°)cos(60°) = √3/21/2 = √3
*Nota: en la escuela podría costarte algún punto escribir así 1√3 (lee Denominadores Racionales), por lo que podría ser mejor utilizar √33
Dibujo rápido
Otra forma de ayudarte a recordar los valores para 30° y 60° es hacer un boceto rápido:
| Dibuja un triángulo equilátero de lado 2 unidades | ||
|
Corta a la mitad. Por Pitágoras, el nuevo lado mide √3 12 + (√3)2 = 22
1 + 3 = 4
|
||
| Luego usa sohcahtoa para sin, cos o tan |
Ejemplo: sen(30°)
Seno: sohcahtoa
Todo el círculo
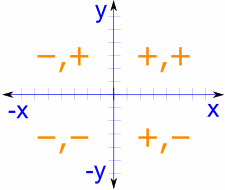
Para todo el círculo necesitamos valores en cada cuadrante, con el correspondiente signo más o menos según las Coordenadas Cartesianas:
Observa que primero va cos y luego sin, por lo que queda (cos, sin):
Ejemplo: ¿Cuánto vale cos(330°) ?
Al hacer un boceto como este, podemos ver que es el valor "largo":√32
Y esta es la misma Circunferencia Unitaria en radianes.
Ejemplo: ¿Cuánto vale sen(7π/6) ?
Primero piensa: "7π/6 = π + π/6", luego haz un boceto.
Entonces podemos ver que es negativo y que es el valor "corto": −½
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
Nota: ¿de dónde salen todos estos valores?Podemos usar la ecuación x2 + y2 = 1 para encontrar las longitudes de x y y (que son iguales a cos y sin cuando el radio es 1):
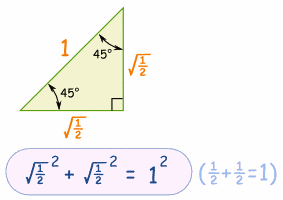
45 GradosPara 45 grados, x y y son iguales, por lo tanto y=x: x2 + x2 = 1
2x2 = 1
x2 = ½
x = y = √(½)
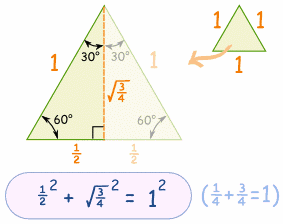
60 GradosConsidera un triángulo equilátero (todos los lados son iguales y todos los ángulos miden 60°) y divídelo por la mitad. El lado "x" ahora mide ½, Y el lado "y" mide: (½)2 + y2 = 1
¼ + y2 = 1
y2 = 1-¼ = ¾
y = √(¾)
30 Grados30° es simplemente igual que 60° con x y y intercambiados, por lo que x = √(¾) y y = ½ Y: √1/2 = √2/4 = √2√4
= √22
También: √3/4 = √3√4
= √32
Y aquí está el resultado (igual que antes):
|