Seno, Coseno y Tangente en los 4 Cuadrantes

Seno, Coseno y Tangente

Las tres funciones principales en trigonometría son Seno, Coseno y Tangente.

triángulo que muestra opuesto, adyacente e hipotenusa

Son fáciles de calcular:

Divide la longitud de un lado de un
triángulo rectángulo entre otro lado

... ¡Pero debemos saber de qué lados!

Para un ángulo θ, las funciones se calculan de esta manera:

Función Seno:	sin(θ) = Opuesto / Hipotenusa
Función Coseno:	cos(θ) = Adyacente / Hipotenusa
Función Tangente:	tan(θ) = Opuesto / Adyacente

Ejemplo: ¿Cuál es el seno de 35°?

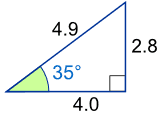Usando este triángulo (las longitudes con solo un decimal):

sin(35°) = Opuesto / Hipotenusa = 2.8/4.9 = 0.57...

Coordenadas Cartesianas

Usando Coordenadas Cartesianas marcamos un punto en una gráfica por lo lejos y lo alto que está:

gráfica con el punto (12,5)
El punto (12,5) está 12 unidades a lo largo y 5 unidades arriba.

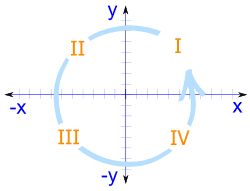
Cuadrantes

Cuatro Cuadrantes

Cuando incluimos valores negativos, los ejes x y y dividen el espacio en 4 partes:

Cuadrantes I, II, III y IV

(Están numerados en sentido antihorario)

En el Cuadrante I tanto x como y son positivas,
en el Cuadrante II x es negativa (y sigue siendo positiva),
en el Cuadrante III tando x como y son negativas, y
en el Cuadrante IV x es nuevamente positiva, y y es negativa.

Así:

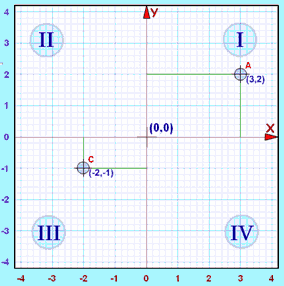
coordenadas cartesianas

Cuadrante	X (horizontal)	Y (vertical)	Ejemplo
I	Positiva	Positiva	(3,2)
II	Negativa	Positiva
III	Negativa	Negativa	(−2,−1)
IV	Positiva	Negativa

Ejemplo: El punto "C" (−2, −1) tiene 2 unidades en dirección negativa y 1 unidad hacia abajo (es decir, dirección negativa).

Tanto x como y son negativas, por lo que ese punto está en el "Cuadrante III"

Seno, Coseno y Tangente en los 4 Cuadrantes

Ahora veamos qué sucede cuando colocamos un triángulo de 30° en cada uno de los 4 Cuadrantes.

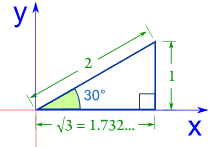
En el Cuadrante I todo es normal y Seno, Coseno y Tangente son todas positivas:

Ejemplo: El seno, coseno y tangente de 30°.

triángulo 30 cuadrante I

Seno	sin(30°) = 1 / 2 = 0.5
Coseno	cos(30°) = 1.732 / 2 = 0.866
Tangente	tan(30°) = 1 / 1.732 = 0.577

Pero en el Cuadrante II, la dirección de x es negativa, y tanto el coseno como la tangente se vuelven negativos:

Ejemplo: Seno, coseno y tangente de 150°

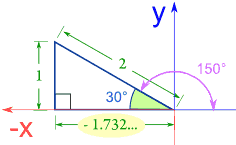
triángulo 30 cuadrante II

Seno	sin(150°) = 1 / 2 = 0.5
Coseno	cos(150°) = −1.732 / 2 = −0.866
Tangente	tan(150°) = 1 / −1.732 = −0.577

En el Cuadrante III, seno y coseno son negativos:

Ejemplo: Seno, coseno y tangente de 210 °

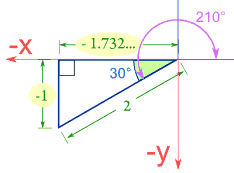
triángulo 30 cuadrante III

Seno	sin(210°) = −1 / 2 = −0.5
Coseno	cos(210°) = −1.732 / 2 = −0.866
Tangente	tan(210°) = −1 / −1.732 = 0.577

Nota: La tangente es positiva porque dividir negativo por negativo da un positivo.

En el Cuadrante IV, seno y tangente son negativos:

Ejemplo: Seno, coseno y tangente de 330°

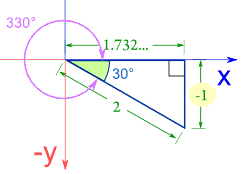
triángulo 30 cuadrante IV

Seno	sin(330°) = −1 / 2 = −0.5
Coseno	cos(330°) = 1.732 / 2 = 0.866
Tangente	tan(330°) = −1 / 1.732 = −0.577

¡Hay un patrón! Mira cuando Seno Coseno y Tangente son positivas ...

Todas son positivas en el Cuadrante I
Seno es la única función positiva en el Cuadrante II
Tangente es la única función positiva en el Cuadrante III
Coseno es la única función positiva en el Cuadrante IV

Esto se puede mostrar aún más fácilmente mediante esta imagen:

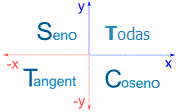
Todas, Seno, Tangente, Coseno

gráfica de funciones trigonométricas

Dos valores

Echa un vistazo a este gráfico de la función Seno:

seno cruza 0.5 en 30,150,390, etc
¡Hay dos ángulos (dentro de los primeros 360°) que tienen el mismo valor!

Y esto también es cierto para Coseno y Tangente.

El problema es: tu calculadora solo te dará uno de esos valores ...

... pero puedes usar estas reglas para encontrar el otro valor:

	Primer valor	Segundo valor
Seno	θ	180º − θ
Coseno	θ	360º − θ
Tangente	θ	θ − 180º

Y si algún ángulo es menor a 0º, entonces suma 360º.

Ahora podemos resolver ecuaciones para ángulos entre 0º y 360º (usando Seno, Coseno y Tangente Inversas)

Ejemplo: Resuelve sin θ = 0.5

Obtenemos la primera solución de la calculadora = sin⁻¹ (0.5) = 30º (está en el Cuadrante I)

La otra solución es 180º − 30º = 150º (Cuadrante II)

Ejemplo: Resuelve tan θ = −1.3

Obtenemos la primera solución de la calculadora = tan⁻¹ (−1.3) = −52.4º

Esto es menor que 0º, entonces sumamos 360º: −52.4º + 360º = 307.6º (Cuadrante IV)

La otra solución es 307.6º − 180º = 127.6º (Cuadrante II)

Ejemplo: Resuelve cos θ = −0.85

Obtenemos la primera solución de la calculadora = cos⁻¹ (−0.85) = 148.2º (Cuadrante II)

La otra solución es 360º − 148.2º = 211.8º (Cuadrante III)

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

Actividad: Una Caminata en el Desierto (2)