Funciones crecientes y decrecientes
Funciones crecientes
Una función está "aumentando" cuando el valor de y aumenta a medida que aumenta el valor de x, así:
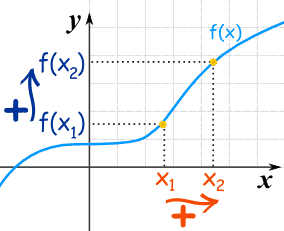
Es fácil ver que y=f (x) tiende a subir a medida que avanza.
¿Planicie?
¿Qué pasa con esa parte plana cerca del comienzo? ¿Eso está bien?- Sí, está bien cuando decimos que la función está aumentando
- Pero no está bien si decimos que la función es estrictamente creciente (no se permite la uniformidad)
Usando álgebra
¿Qué pasa si no podemos trazar la gráfica para ver si está aumentando? En ese caso, necesitamos una definición usando álgebra.Para una función y=f(x):
| cuando x1 < x2, si f(x1) ≤ f(x2) | Creciente | |
| cuando x1 < x2, si f(x1) < f(x2) | Estrictamente creciente |
Eso tiene que ser cierto para cualquier x1, x2, no solo para algunos valores que pudiéramos elegir.
Las partes importantes son los signos < y ≤ ... ¡recuerda dónde van!
Un ejemplo:
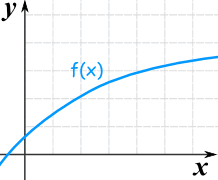 |
| Esta es también una función creciente aunque la tasa de crecimiento se reduce |
Para un intervalo
Por lo general, solo nos interesa algún intervalo, como este:
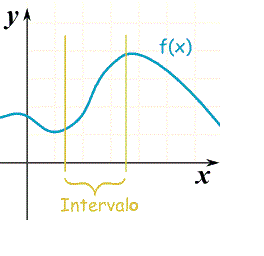
Esta función aumenta para el
intervalo mostrado
(puede estar aumentando o disminuyendo en otros lugares)
Funciones decrecientes
El valor de y decrece a medida que aumenta el valor de x:
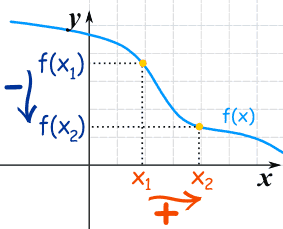
Para una función y=f(x):
| cuando x1 < x2, si f(x1) ≥ f(x2) | Decreciente | |
| cuando x1 < x2, si f(x1) > f(x2) | Estrictamente decreciente |
Observa que f(x1) ahora es mayor que (o igual a) f(x2).
Un ejemplo
Intentemos encontrar dónde aumenta o disminuye una función.
Ejemplo: f(x) = x3−4x, para x en el intervalo [−1,2]
Dibujémosla, incluyendo el intervalo [−1,2]:
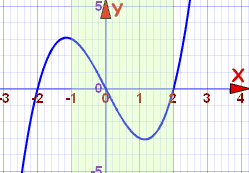
A partir de −1 (el comienzo del intervalo [−1,2]):
- en x = −1 la función está disminuyendo,
- continúa disminuyendo hasta aproximadamente 1.2
- luego aumenta desde allí, más allá de x = 2
Dentro del intervalo [−1,2]:
- la curva disminuye en el intervalo [−1, aprox 1.2]
- la curva aumenta en el intervalo [aprox 1.2, 2]
Funciones constantes
Una función constante es una línea horizontal:
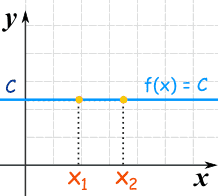
Rectas
De hecho, las líneas aumentan, disminuyen o son constantes.
La ecuación de una recta es:
y = mx + b

La pendiente m nos dice si la función es creciente, decreciente o constante:
| m < 0 | decreciente | |
| m = 0 | constante | |
| m > 0 | creciente |
Uno a uno
Las funciones estrictamente crecientes (y estrictamente decrecientes) tienen una propiedad especial llamada "inyectiva" o "uno a uno" que simplemente significa que nunca obtenemos el mismo valor "y" dos veces.
Función General
"Inyectiva" (uno a uno)
¿Por qué es útil esto? ¡Porque las funciones inyectivas se pueden invertir!
Podemos volver de un valor "y" a un valor "x" (lo
cual no podemos hacer cuando hay más de un posible valor "x").
Lee Inyectivo, sobreyectivo y biyectivo para saber más.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
