La Fórmula de Euler
(Hay otra "Fórmula
de Euler" sobre números complejos,
esta página es sobre la que se usa en Geometría y Grafos)
La Fórmula de Euler
Para cualquier poliedro que no se intersecta a sí mismo, el
- Número de Caras
- más el Número de Vértices (esquinas)
- menos el Número de Aristas
siempre es igual a 2
Esto se puede escribir así: C + V − A = 2
 |
Usa la fórmula en el cubo: 6 + 8 − 12 = 2 |
Ejemplo con los sólidos platónicos
Probemos con los 5 sólidos platónicos:
| Nombre | Caras | Vértices | Aristas | C+V-A | |
|---|---|---|---|---|---|
| Tetraedro |  |
4 | 4 | 6 | 2 |
| Cubo | |
6 | 8 | 12 | 2 |
| Octaedro |  |
8 | 6 | 12 | 2 |
| Dodecaedro |  |
12 | 20 | 30 | 2 |
| Icosaedro |  |
20 | 12 | 30 | 2 |
(De hecho, la Fórmula de Euler se puede utilizar para demostrar que solo hay 5 Sólidos Platónicos)
|
¿Por qué siempre 2? 7 + 8 − 13 = 2 |
 |
|
O intenta incluir otro vértice, 6 + 9 − 13 = 2. |
 |
| "No importa lo que hagamos, siempre
terminamos con 2" (Pero solo para este tipo de Poliedros ... ¡sigue leyendo!) |
La esfera
Todos los sólidos platónicos (y muchos otros sólidos) son como una Esfera ... podemos remodelarlos para que se conviertan en una Esfera (mueve sus puntos de esquina, luego curva sus caras un poco).
Por esta razón sabemos que C + V − A = 2 para una
esfera
(Ten cuidado, no podemos decir simplemente que una esfera tiene 1 cara y 0 vértices y aristas, porque C+V−A=1)
Entonces, el resultado es 2 nuevamente.
¡Pero no siempre es 2 ...!
Ahora que ves cómo funciona esto, descubramos cuando no funciona.
¿Y si unimos dos esquinas opuestas de un icosaedro?
Sigue siendo un icosaedro (pero ya no es convexo).
De hecho, se parece un poco a un tambor en el que alguien ha cosido la
parte superior y la inferior.
Ahora, hay el mismo número de aristas y caras ... ¡pero un
vértice menos!
Entonces:
C + V − A = 1
¡Oh no! No siempre la suma es 2.
La razón por la que no funcionó fue que esta nueva forma es básicamente diferente ... esa unión en el medio significa que dos vértices se reducen a 1.
La Característica de Euler
Entonces, C+V−A puede ser igual a 2, o 1, y tal vez a otros valores, por lo que la fórmula más general es
C + V − A = χ
Donde χ se conoce como "La Característica de Euler".
Aquí hay algunos ejemplos:
| Forma | χ | |
|---|---|---|
| Esfera |  |
2 |
| Toro |  |
0 |
| Banda de Moebius |  |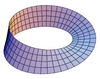
0 |
Y la característica de Euler también puede ser menor que cero.
Este es el "Cubohemioctaedro": Tiene 10 Caras (puede parecer más, pero
algunas de las caras "internas" son en realidad una sola cara), 24
Aristas y 12 Vértices, entonces:
C + V − A = −2
De hecho, la Característica de Euler es una idea básica en Topología (el estudio de la naturaleza del Espacio).
Una taza y una dona
(Animación por cortesía del
usuario de Wikipedia:Kieff)
Por último, esta discusión estaría incompleta sin mostrar que una dona
(rosquilla) y una taza de café son realmente lo mismo.
Bueno, se pueden deformar entre sí.
Decimos que los dos objetos son "homeomorfos" (del griego homoios =
idéntico y morphe = forma)
Al igual que los sólidos platónicos son homeomorfos a la esfera.
Y tu cuerpo es homeomorfo a un toro si aprietas la nariz.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
