Teorema de Pitágoras
|
Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos:
... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos! |
El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)
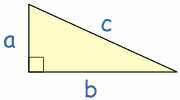 |
Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a2 + b2 = c2 |
¿Seguro... ?
Veamos si funciona con un ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, así que la fórmula debería funcionar.
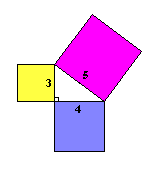 |
Veamos si las áreas son la misma: 32 + 42 = 52 Calculando obtenemos: 9 + 16 = 25 ¡sí, funciona! |
¿Por qué es útil esto?
Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (¡Pero recuerda que sólo funciona en triángulos rectángulos!)
¿Cómo lo uso?
Escríbelo como una ecuación: |
a2 + b2 = c2 |
Ahora puedes usar álgebra para encontrar el valor que falta, como en estos ejemplos:
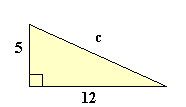
|
a2 + b2 = c2 52 + 122 = c2 25 + 144 = 169 c2 = 169 c = √169 c = 13 |
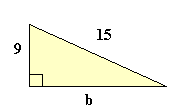
a2 + b2 = c2 92 + b2 = 152 81 + b2 = 225 Resta 81 a ambos lados b2 = 144 b = √144 b = 12 |
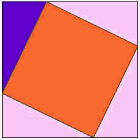
¡Y Puedes Demostrarlo Tú Mismo!
| Consigue papel y tijeras, y usa la siguiente animación como guía: | |
|
|
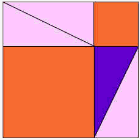
Otra Demostración, Muy Simple
| Aquí tienes una de las demostraciones más antiguas de que el cuadrado grande tiene la misma área que los otros cuadrados juntos. | |||||
|
|||||
También tenemos una demostración sumando las áreas.
| Nota histórica: aunque se llama Teorema de Pitágoras, ¡también lo conocían los matemáticos indios, griegos, chinos y babilonios antes de que él viviera! |