Números binarios, decimales y hexadecimales
Decimales
Para entender los números binarios y hexadecimales, lo mejor es entender bien cómo funcionan los números decimales.
Cada dígito de un número decimal va en una "posición", y el punto decimal nos dice qué posición es cada una.
La posición justo a la izquierda del punto son las "unidades". Cada vez que nos movemos a la izquierda vale 10 veces más, y a la derecha vale 10 veces menos:
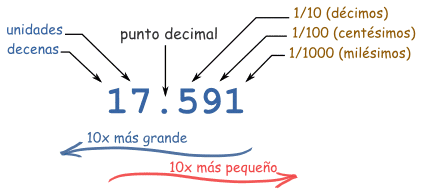
Pero esto sólo es una manera de escribir números. Hay otras maneras como los números romanos, binarios, hexadecimales, y más. ¡Incluso podrías marcar puntos en una hoja de papel!
Contar en diferentes sistemas de numeración
El sistema decimal de numeración también se llama "base 10", porque se basa en el número 10.
En decimal hay diez símbolos (0 a 9), pero fíjate en esto: no hay un símbolo para el "diez". "10" son en realidad dos símbolos juntos, un "1" y un "0":
En decimal contamos 0,1,2,3,4,5,6,7,8,9, entonces decimos "me he quedado sin símbolos, así que empiezo otra vez con 0, pero primero voy a añadir 1 a la izquierda".
En decimal contamos 0,1,2,3,4,5,6,7,8,9, entonces decimos "me he quedado sin símbolos, así que empiezo otra vez con 0, pero primero voy a añadir 1 a la izquierda".
Pero no es obligatorio usar 10 como "base". Podrías usar 2 ("binario"), 16 ("hexadecimal"), ¡o cualquier número que quieras! Sólo sigue la misma regla:
Cuenta hasta justo antes de la "base", después vuelve al 0, pero añadiendo 1 a la izquierda.
¿Por qué no pruebas tú? Intenta contar puntos con bases 2 a 16 en esta pequeña demostración:
| JAVASCRIPT |
| Prueba esto: después de elegir una base y dejar que trabaje un rato, usa el botón de "Pausa" y mira si ha acertado el número de puntos, como en este ejemplo en base 2: | 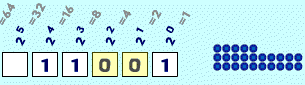 |
| Ejemplo: | 1×16 + 1×8 + 1×1 = 16+8+1 = 25 |
Números binarios
Los números binarios son en "base 2" en lugar de "base 10". Empiezas contando 0, después 1, ¡ya se te acabaron los dígitos! Así que vuelves al 0, pero aumentas en 1 el número de la izquierda.
Funciona así:
|
000
|
|
|
001
|
|
|
010
|
no hay "2" en binario, así que volvemos al 0... ... y sumamos 1 a la cifra de la izquierda |
|
011
|
|
|
100
|
volvemos otra vez al 0, y sumamos 1 a la izquierda... ... pero ese número ya es 1 así que vuelve a ser 0... ... y el 1 se suma al siguiente número a la izquierda |
|
101
|
|
|
110
|
etc... |
Números hexadecimales
Los números hexadecimales son interesantes. ¡Hay 16 dígitos diferentes! Son como los decimales hasta el 9, pero después hay letras ("A',"B","C","D","E","F") para los valores de 10 a 15.
Así que con una sola cifra hexadecimal se pueden dar 16 valores diferentes en lugar de los 10 de siempre:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hexadecimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |

