Hexadecimales
Un número hexadecimal es en base 16
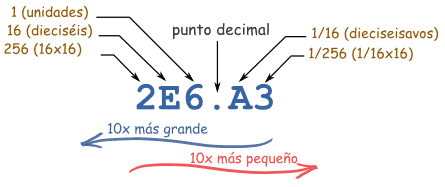 |
| Este es 2×16×16 + 14×16 + 6 + 10/16 + 3/(16×16) Lee más abajo para averiguar por qué |
Cada cifra se pone a la izquierda o derecha del punto, para indicar valores más grandes o más pequeños que uno:
| La que está justo a la izquierda del punto es un número entero, y a esa posición la llamamos unidades. Cuando nos movemos a la izquierda, cada posición vale 16 veces más. |
|
| La primera cifra a la izquierda del punto vale un dieciseisavo (1/16). Cuando nos movemos a la derecha, cada posición vale 16 veces menos (un dieciseisavo de la anterior). |
16 valores diferentes
Los números hexadecimales son como los números decimales hasta el 9, pero también se usan letras ("A',"B","C","D","E","F") para los valores 10 a 15:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hexadecimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Así que un dígito hexadecimal puede tomar 16 valores diferentes en lugar de 10.
Definición de hexadecimal
| La palabra "hexadecimal" quiere decir "en base 16" (Del griego hexa: "seis" y del latín decima: "la décima parte"). |
Ejemplos
Ejemplo 1: ¿Cuánto es 2E6 (hexadecimal)?
- El "2" está en la posición de "16×16", así que vale 2×16×16
- La "E" está en la posición de "16", así que vale 14×16
- El "6" está en la posición de las "unidades" así que vale 6.
- Respuesta: 2E6 = 2×16×16 + 14×16 + 6 (=742 en decimal)
Ejemplo 2: ¿Cuánto es 2.3 (hexadecimal)?
- A la izquierda del punto hay "2", esa es la parte entera.
- El 3 está en la posición de los "dieciseisavo", así que vale "3 dieciseisavos", que son 3/16
- Así, 2.3 es "2 y 3 dieciseisavos" (=2.1875 en decimal)

