Ecuación de la Recta Usando 2 Puntos
Primero, veámosla en acción. Aquí hay dos puntos (puedes arrastrarlos) y la ecuación de la línea a través de ellos. La explicación viene después.
Los puntos
Usamos Coordenadas Cartesianas para marcar un punto en una gráfica para indicar qué tan lejos y qué tan arriba está:
Ejemplo: el punto (12,5) tiene 12 unidades a lo largo y 5
unidades arriba
Pasos a seguir
Hay 3 pasos para encontrar la Ecuación de la Línea Recta:
- 1. Encuentra la pendiente de la recta
- 2. Pon la pendiente y un punto en la "Fórmula Punto-Pendiente"
- 3. Simplifica
Paso 1: Encuentra la pendiente (o gradiente) desde 2 puntos
¿Cuál es la pendiente (o gradiente) de esta línea?
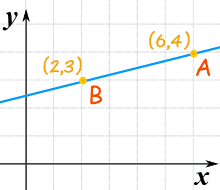
Conocemos dos puntos:
- el punto "A" es (6,4) (en x es 6, y es 4)
- el punto "B" es (2,3) (en x es 2, y es 3)
Mira este diagrama ...
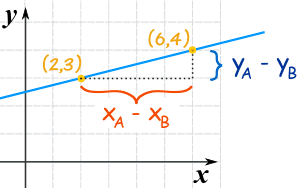
Pendiente m = cambio en ycambio en x = yA − yBxA − xB
En otras palabras, nosotros:- restamos los valores de Y,
- restamos los valores X
- luego dividimos
Así:
m = cambio en y cambio en x = 4−3 6−2 = 1 4 = 0.25
No importa qué punto se use primero, el resultado sigue siendo el mismo. Intenta intercambiar los puntos:
m = cambio en y cambio en x = 3−4 2−6 = −1 −4 = 0.25
Es la misma respuesta.
Paso 2: La "Fórmula Punto-Pendiente"
Ahora coloca esa pendiente y un punto en la "Fórmula Punto-Pendiente".

Empieza con la fórmula "punto-pendiente" (donde x1 y y1 son las coordenadas de un punto en la recta):
y − y1 = m(x − x1)
Podemos elegir cualquier punto de la recta para x1 y y1, así que usemos el punto (2,3):
y − 3 = m(x − 2)
Ya calculamos la pendiente "m":
m = cambio en ycambio en x = 4−36−2 = 14
Y tenemos:
y − 3 = 14(x − 2)
Esa ya es una respuesta, pero podemos simplificarla aún más.
Paso 3: Simplificar
Y obtenemos:
y = x4 + 52
Que ahora está en la forma Pendiente-Intersección (y = mx + b).
¡Compruébalo!
Confirmemos probando con el segundo punto (6,4):
y = x/4 + 5/2 = 6/4 + 2.5 = 1.5 + 2.5 = 4
Sí, cuando x=6 entonces y=4, ¡así que funciona!
Otro ejemplo
Ejemplo: ¿Cuál es la ecuación de esta recta?
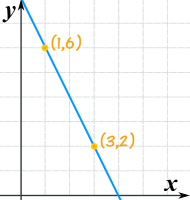
Empieza con la fórmula "punto-pendiente":
y − y1 = m(x − x1)
Introduce estos valores:
- x1 = 1
- y1 = 6
- m = (2−6)/(3−1) = −4/2 = −2
Y obtenemos:
y − 6 = −2(x − 1)
Simplificamos a la forma Pendiente-Intersección (y = mx + b):
y − 6 = −2x + 2
y = −2x + 8
¡HECHO!
La gran excepción
El método anterior funciona muy bien excepto por un caso particular: una línea vertical:
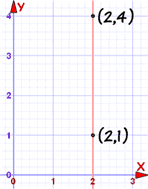
|
La pendiente de una línea vertical no está definida (porque no podemos dividir por 0): m = yA − yBxA − xB = 4 − 12 − 2 = 30 = indefinido Pero todavía hay una forma de escribir la ecuación: usa x= en lugar de y=, de esta manera: x = 2 |
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

