Introducción a la Trigonometría
Trigonometría (del Griego trigōnos "triángulo" + metron "medida")
¿Quieres aprender trigonometría? Aquí hay un resumen
rápido.
Sigue los enlaces para obtener más información o ve a Índice
de Trigonometría
| Trigonometría ... se trata de los triángulos. |
¡La trigonometría nos ayuda a encontrar ángulos y distancias, y se usa mucho en ciencia, ingeniería, videojuegos y más!
Triángulo Rectángulo
El triángulo de mayor interés es el triángulo rectángulo. El ángulo recto se muestra en la pequeña caja en la esquina:
Uno de los otros ángulos normalmente se denomina θ, y los tres lados se llaman:
- Adyacente: adyacente (al lado de) al ángulo θ
- Opuesto: opuesto al ángulo θ
- y el lado más largo es la Hipotenusa
¿Por qué un triángulo rectángulo?
¿Por qué es tan importante este triángulo?
Imagina que podemos medir a lo largo y hacia arriba pero queremos saber la distancia directa y el ángulo:
O podríamos tener una distancia y un ángulo y necesitar "trazar el punto" a lo largo y hacia arriba:
¡Y la trigonometría da las respuestas!
Seno, Coseno y Tangente
Las funciones principales en trigonometría son Seno, Coseno y Tangente
Estas funciones son simplemente un lado de un triángulo rectángulo dividido por otro.
Para todo ángulo "θ":
(Seno, coseno y tangente a menudo se abrevian como sen (o sin), cos y tan.)
Ejemplo: ¿Cuál es el seno de 35°?
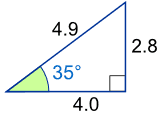
Usando este triángulo (las longitudes están redondeadas a un decimal):
sen(35°) = OpuestoHipotenusa = 2.84.9 = 0.57...
Las calculadoras tienen sin, cos y tan para ayudarnos, así que veamos cómo usarlas:
Ejemplo: ¿Qué tan alto es el árbol?
No podemos alcanzar la cima del árbol, así que nos alejamos y medimos un ángulo (usando un transportador) y una distancia (usando un láser):
- Conocemos la Hipotenusa
- Y queremos encontrar el Opuesto
Seno es la proporción Opuesto/Hipotenusa:
sen(45°) = Opuesto Hipotenusa

Ten a la mano una calculadora, presiona la tecla "sin" y luego escribe "45":
sin(45°) = 0.7071...
¿Qué significa el 0.7071 ...? Es la proporción de las longitudes de los lados, por lo que el Opuesto es aproximadamente 0.7071 veces el largo de la Hipotenusa.
Ahora podemos poner 0.7071 ... en lugar de sin(45°):
0.7071... = Opuesto Hipotenusa
Y también sabemos que la hipotenusa es 20:
0.7071... = Opuesto 20
Para resolver, primero multiplica ambos lados por 20:
20 × 0.7071... = Opuesto
Finalmente:
Opuesto = 14.14m (a 2 decimales)
Ejemplo: ¿Qué tan alto es el árbol?
El árbol tiene 14.14m de altura
Prueba Sen, Cos y Tan
Juega con esto un rato (mueve el cursor) y familiarízate con los valores de seno, coseno y tangente para diferentes ángulos, como 0°, 30°, 45°, 60° y 90°.
También prueba con 120°, 135°, 180°, 240°, 270° etc, y observa que las posiciones pueden ser positivas o negativas de acuerdo con las reglas de las Coordenadas Cartesianas, entonces el seno, el coseno y la tangente cambian entre positivo y negativo también.
¡Entonces la trigonometría también se trata de círculos!
Círculo Unitario
Con lo que acabas de jugar es el Círculo Unitario.
Es un círculo con un radio de 1 y su centro en 0.Como el radio es 1, podemos medir directamente seno, coseno y tangente.
Aquí vemos la función seno trazada por el círculo unitario:
Nota: puedes ver las gráficas de las funciones seno, coseno y tangente.
Grados y Radianes
Los ángulos pueden medirse en Grados o Radianes. Aquí hay unos ejemplos:
| Ángulo | Grados | Radianes |
|---|---|---|
| 90° | π/2 | |
| __ Ángulo llano | 180° | π |
| 360° | 2π |
Patrón Repetitivo
Debido a que el ángulo gira alrededor del círculo, las funciones seno, coseno y tangente se repiten una vez cada rotación completa (ver Amplitud, Periodo, Desfase y Frecuencia).
Cuando deseamos calcular la función para un ángulo mayor que una rotación completa de 360° (2π radianes), restamos tantas rotaciones completas como sea necesario para que vuelva a estar por debajo de 360° (2π radianes):
Ejemplo: ¿Cuál es el coseno de 370°?
370° es mayor que 360° así que restaremos 360°
370° − 360° = 10°
cos(370°) = cos(10°) = 0.985 (a 3 decimales)
Y cuando el ángulo es menor que cero, simplemente suma rotaciones completas.
Ejemplo: ¿Cuál es el seno de −3 radianes?
−3 es menor que 0, así que sumemos 2π radianes
−3 + 2π = −3 + 6.283... = 3.283... radianes
sin(−3) = sin(3.283...) = −0.141 (a 3 decimales)
Resolviendo Triángulos
La trigonometría también es útil para triángulos generales, no solo
para triángulos rectángulos.
Nos ayuda a Resolviendo
Triángulos. "Resolver" significa encontrar lados y ángulos
faltantes.
Ejemplo: Encuentra el ángulo faltante "C"
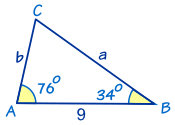
El ángulo C puede hallarse usando que la suma de los ángulos internos de todo triángulo es 180°:
Así que C = 180° − 76° − 34° = 70°
También podemos encontrar las longitudes laterales faltantes. La regla general es:
Cuando conocemos 3 datos, ya sean lados o ángulos,
podemos encontrar los otros 3
(excepto cuando solo conoces los tres ángulos)
Lee Resolviendo Triángulos para más detalles.
Otras Funciones (Cotangente, Secante, Cosecante)
Similar a Seno, Coseno y Tangente, hay otras tres funciones trigonométricas que se consiguen dividiendo un lado entre otro:
|
Función Cosecante:
|
csc(θ) = Hipotenusa / Opuesto |
|
Función Secante:
|
sec(θ) = Hipotenusa / Adyacente |
|
Función Cotangente:
|
cot(θ) = Adyacente / Opuesto |
Trigonometría e Identidades de Triángulos
Y a medida que mejores en la Trigonometría, puedes aprender estas:
 |
Las Identidades Trigonométricas son ecuaciones que son verdaderas para todos los triángulos rectángulos. |
|
Las Identidades de los Triángulos son ecuaciones que son verdaderas para todos los triángulos (no tienen que tener un ángulo recto). |
¡Disfruta convirtiéndote en un experto en triángulos (y círculos)!

