Introducción a la Integración
La integración es una forma de sumar porciones para encontrar el todo.
La integración se puede utilizar para encontrar áreas, volúmenes, puntos centrales y muchas cosas útiles. Pero es más fácil comenzar por encontrar el área debajo de la curva de una función como esta:
¿Cuál es el área?
Porciones (o rebanadas)
Y escribimos dx para indicar que las porciones Δx se acercan a cero en ancho.
¡Esas son muchas cosas para sumar!
Pero no tenemos que sumar individualmente cada porción, ya que hay un "atajo". Porque ...
... encontrar una integral es lo inverso de encontrar una derivada.
(¡Entonces realmente deberías saber sobre Derivadas antes de seguir leyendo!)
Como se muestra aquí:
Ejemplo: ¿Cuál es la integral de 2x?
La integral de 2x es x2 ...
... porque la derivada de x2 es 2x
*Ya hablaremos del "+C" más adelante.
Ese sencillo ejemplo puede confirmarse calculando el área:
Área del triángulo = 12(base)(altura) = 12(x)(2x) = x2
¡A veces la integración puede ser así de sencilla!
Notación
Después del Símbolo de Integral colocamos la función de la cual
queremos encontrar la integral (llamada Integrando).
Y luego se termina con dx para significar que los cortes van
en la dirección x (y tienen un ancho cercano a cero).
Y así es como escribimos la respuesta:
Más C
La respuesta se escribió como x2, pero, ¿por qué + C ?
Es la "constante de integración". Está ahí debido a todas las funciones cuya derivada es 2x:
La derivada de x2+4 es 2x, y la derivada
de x2+99 también es 2x, etcétera. Esto es
así porque la derivada de una constante es cero.
Entonces, cuando invertimos la operación (para encontrar la
integral) solo conocemos 2x, pero podría haber habido una constante de
cualquier valor.
Así que concluimos esta idea escribiendo + C
al final.
Grifo y tanque
La integración es como llenar un tanque con un grifo.
La entrada (antes de la integración) es el flujo del
grifo.
Integrar el flujo (sumando todos los chorritos de agua) nos da el volumen
de agua en el tanque.
Imagina un flujo constante de 1:
La integral de 1 es x
Con una tasa de flujo de 1 litro por segundo, el volumen aumenta en 1 litro cada segundo, así que aumentará en 10 litros después de 10 segundos, 60 litros después de 60 segundos, y así sucesivamente.
La tasa de flujo se mantiene en 1, y el volumen aumenta en x
Y también funciona al revés:
Si el volumen del tanque aumenta en x, entonces la tasa de
flujo debe ser 1.
La derivada de x es 1
¡Esto muestra que las integrales y las derivadas son opuestas!
Ahora, con una tasa de flujo creciente
Imagina que el flujo comienza en 0 y va aumentando gradualmente (quizás un motor abre la llave lentamente):
A medida que la tasa de flujo aumenta, el tanque se llena cada vez más rápido:
- Integración: Con una tasa de flujo de 2x, el volumen del tanque aumenta en x2
- Derivada: Si el volumen del tanque aumenta en x2, entonces la tasa de flujo debe ser 2x
Podemos escribirlo de esta forma:
Y mira, ¡hasta obtenemos una buena explicación de ese valor “C”! ... tal vez el tanque ya tenía agua desde el principio.
- El flujo aún incrementa el volumen en la misma cantidad
- Y el aumento de volumen puede devolvernos la tasa de flujo
Lo cual nos enseña a recordar siempre el “+C”.
Otras funciones
Bueno, ya hemos jugado con y=2x lo suficiente, entonces,
¿cómo integramos otras funciones?
Si tenemos la suerte de encontrar la función en el lado del resultado
de una derivada, entonces (sabiendo que las derivadas y las
integrales son opuestas) tenemos una respuesta. Pero recuerda agregar
C.
Ejemplo: ¿Cuál es ∫cos(x) dx ?
De la Tabla de Reglas de Derivación vemos que la derivada de sin(x) es cos(x), entonces:
∫cos(x) dx = sin(x) + C
Pero gran parte de este proceso "inverso" ya se ha realizado (ver Reglas de Integración).
Ejemplo: ¿Cuál es ∫x3 dx ?
En las Reglas de Integración hay una "Regla de las Potencias" que dice:
∫xn dx = xn+1n+1 + C
Podemos usar esa regla con n=3:
∫x3 dx = x44 + C
Saber cómo usar esas reglas es la clave para ser bueno en Integración.
Así que aprende esas reglas y practica mucho.
¡Aprende las Reglas
de Integración y practica! ¡Practica! ¡Practica!
(hay algunas preguntas a continuación para que comiences)
Integrales Indefinidas vs Definidas
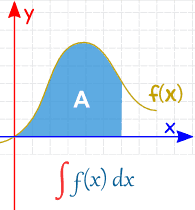
Hemos estado haciendo Integrales Indefinidas hasta
ahora.
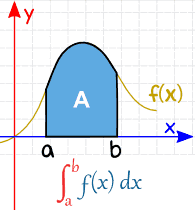
Una Integral Definida tiene
valores para calcular (se colocan en la parte inferior y superior de
la "S"):
 |
 |
|
| Integral Indefinida | Integral Definida |
Lee Integrales Definidas para saber más.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
