Distribución Normal
Los datos se pueden "distribuir" (esparcir) de diferentes maneras.
O más a la derecha
Sesgados a la derecha
Pero en muchos casos los datos tienden a ubicarse alrededor de un valor central, sin sesgo a la izquierda o derecha, y se aproximan a una "Distribución Normal" como esta:
La curva azul es una Distribución Normal.
El histograma amarillo muestra algunos datos que
la siguen de cerca, pero no perfectamente (lo cual es normal).
 |
A menudo se le llama "Curva de Campana" porque parece una campana. |
Muchas cosas siguen de cerca una Distribución Normal:
- alturas de personas
- tamaño de productos fabricados
- errores de medición
- presión arterial
- puntuaciones en exámenes
Decimos que los datos están "distribuidos normalmente":
La Distribución Normal tiene:
Quincunce
¡Puedes ver una distribución normal creándose por puro azar!
Se llama el Quincunce y es una máquina increíble. ¡Pruébala!
Desviaciones Estándar
La Desviación Estándar es una medida de qué tan dispersos están los números (lee esa página para ver detalles sobre cómo calcularla).
Cuando calculamos la desviación estándar encontramos que aproximadamente:
1 desviación estándar de la media
2 desviaciones estándar de la media
3 desviaciones estándar de la media
Ejemplo: El 95% de los estudiantes de una escuela miden entre 1.1m y 1.7m de estatura.
Suponiendo que estos datos se distribuyen normalmente, ¿puedes calcular la media y la desviación estándar?
La media está a mitad de camino entre 1.1m y 1.7m:
Media = (1.1m + 1.7m) / 2 = 1.4m
El 95% corresponde a 2 desviaciones estándar a cada lado de la media (un total de 4 desviaciones estándar), por lo que:
| 1 desviación estándar | = (1.7m-1.1m) / 4 |
| = 0.6m / 4 | |
| = 0.15m |
Y este es el resultado:
Es bueno conocer la desviación estándar, porque (para datos que son aproximadamente normales) podemos decir que cualquier valor es:
- probable que esté dentro de 1 desviación estándar (68 de cada 100 deberían estarlo)
- muy probable que esté dentro de 2 desviaciones estándar (95 de cada 100 deberían estarlo)
- casi con total certeza estará dentro de 3 desviaciones estándar (997 de cada 1000 deberían estarlo)
Puntuaciones Estándar (Puntajes z)
Al número de desviaciones estándar respecto a la media también se le llama "Puntuación Estándar" o "puntaje z" (z-score). ¡Acostúmbrate a esas palabras!
- σ (sigma) es la desviación estándar
- z es la puntuación estándar (cuántas desviaciones estándar respecto a la media)
Ejemplo: En esa misma escuela uno de tus amigos mide 1.85m de estatura
Puedes ver en la curva de campana que 1.85m está a 3 desviaciones estándar de la media de 1.4, por lo que:
La estatura de tu amigo tiene un "puntaje z" de 3.0
También es posible calcular cuántas desviaciones estándar está 1.85 de la media
¿A qué distancia está 1.85 de la media?
Está a 1.85 - 1.4 = 0.45m de la media
¿Cuántas desviaciones estándar es eso? La desviación estándar es 0.15m, así que:
0.45m / 0.15m = 3 desviaciones estándar
Para convertir un valor a una Puntuación Estándar ("puntaje z"):
- primero resta la media,
- luego divide entre la Desviación Estándar
Y hacer eso se llama "Estandarizar":
Podemos tomar cualquier Distribución Normal y convertirla en la Distribución Normal Estándar.
Ejemplo: Tiempo de viaje
Una encuesta sobre el tiempo de viaje diario tuvo estos resultados (en minutos):
26, 33, 65, 28, 34, 55, 25, 44, 50, 36, 26, 37, 43, 62, 35, 38, 45, 32, 28, 34
La Media es 38.8 minutos y la Desviación Estándar es 11.4 minutos (puedes copiar y pegar los valores en la Calculadora de Desviación Estándar si quieres).
Convierte los valores a puntajes z ("puntuaciones estándar").
Para convertir 26:
Por lo tanto, 26 está a −1.12 Desviaciones Estándar de la Media
Aquí están las tres primeras conversiones
| Valor original | Cálculo | Puntuación estándar (puntaje z) |
| 26 | (26-38.8) / 11.4 = | −1.12 |
| 33 | (33-38.8) / 11.4 = | −0.51 |
| 65 | (65-38.8) / 11.4 = | +2.30 |
| ... | ... | ... |
Y aquí están gráficamente:
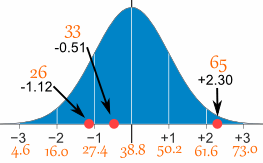
¡Puedes calcular el resto de los puntajes z tú mismo!
La fórmula del puntaje z que hemos estado usando es:
z = x − μσ
- z es el "puntaje z" (Puntuación Estándar)
- x es el valor a estandarizar
- μ ("mu") es la media
- σ ("sigma") es la desviación estándar
Y así es como se usa:
Ejemplo: Tiempo de viaje (continuación)
Aquí están las tres primeras conversiones usando la "fórmula del puntaje z":
z = x − μσ
- μ = 38.8
- σ = 11.4
| x | x − μσ | z (puntaje z) |
|---|---|---|
| 26 | 26 − 38.811.4 | = −1.12 |
| 33 | 33 − 38.811.4 | = −0.51 |
| 65 | 65 − 38.811.4 | = +2.30 |
| ... | ... | ... |
Los cálculos exactos que hicimos antes, solo siguiendo la fórmula.
¿Por qué estandarizar...?
Puede ayudarnos a tomar decisiones sobre nuestros datos.
Ejemplo: El profesor Willoughby está calificando un examen.
Aquí están los resultados de los estudiantes (sobre 60 puntos):
20, 15, 26, 32, 18, 28, 35, 14, 26, 22, 17
La mayoría de los estudiantes ni siquiera obtuvieron 30 de 60, y la mayoría reprobará.
El examen debió ser realmente difícil, por lo que el profesor decide estandarizar todos los puntajes y reprobar únicamente a las personas que estén a más de 1 desviación estándar por debajo de la media.
La Media es 23 y la Desviación Estándar es 6.6, y estos son los Puntajes Estándar:
-0.45, -1.21, 0.45, 1.36, -0.76, 0.76, 1.82, -1.36, 0.45, -0.15, -0.91
Ahora solo 2 estudiantes van a reprobar (los que están por debajo de −1 desviación estándar)
¡Mucho más justo!
También facilita las cosas porque solo necesitamos una tabla (la Tabla de Distribución Normal Estándar), en lugar de hacer cálculos individualmente para cada combinación de media y desviación estándar.
En más detalle
Aquí está la Distribución Normal Estándar con porcentajes para cada media desviación estándar, y porcentajes acumulados:
Ejemplo: Tu puntuación en una prueba reciente fue de 0.5 desviaciones estándar por encima del promedio, ¿cuántas personas obtuvieron una calificación más baja que tú?
- Entre 0 y 0.5 es 19.1%
- Menos de 0 es 50% (mitad izquierda de la curva)
Por lo tanto, el total con menor puntuación que tú es:
50% + 19.1% = 69.1%
En teoría, el 69.1% obtuvo una puntuación menor que tú (pero con datos reales el porcentaje puede ser diferente)
Un ejemplo práctico: tu empresa empaca azúcar en bolsas de 1 kg.
Cuando pesas una muestra de bolsas obtienes estos resultados:
- 1007g, 1032g, 1002g, 983g, 1004g, ... (cien mediciones)
- Media = 1010g
- Desviación Estándar = 20g
Algunos valores son menores que 1000g ... ¿puedes solucionar eso?
La distribución normal de tus mediciones se ve así:
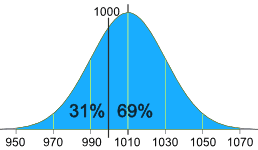
El 31% de las bolsas tienen menos de 1000g,
¡lo que perjudica al cliente!
Es algo aleatorio, por lo que no podemos evitar que haya bolsas con menos de 1000g, pero podemos intentar reducirlo mucho.
Ajustemos la máquina para que 1000g esté ...
... a −3 desviaciones estándar:
... a −2.5 desviaciones estándar:
Así que ajustemos la máquina para tener 1000g a −2.5 desviaciones estándar de la media.
Ahora, podemos ajustarla para:
- aumentar la cantidad de azúcar en cada bolsa (lo que cambia la media), o
- hacerla más precisa (lo que reduce la desviación estándar)
Probemos ambas opciones.
Ajustar la cantidad media en cada bolsa
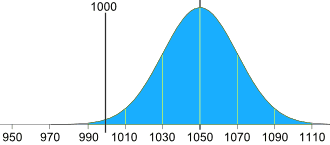
La desviación estándar es 20g, y necesitamos 2.5 de ellas:
2.5 × 20g = 50g
Por lo tanto, la máquina debería tener un promedio de 1050g, así:
Ajustar la precisión de la máquina
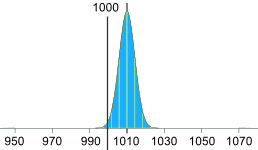
O podemos mantener la misma media (de 1010g), pero entonces necesitamos que 2.5 desviaciones estándar sean iguales a 10g:
10g / 2.5 = 4g
Por lo tanto, la desviación estándar debería ser de 4g, así:
(¡Esperemos que la máquina sea así de precisa!)
O tal vez podríamos tener alguna combinación de mayor precisión y un tamaño promedio ligeramente mayor, ¡eso te lo dejo a ti!
Valores más precisos ...
Usa la Tabla de Distribución Normal Estándar cuando quieras valores más precisos.