Ecuación de la Recta Punto-Pendiente
La forma "punto-pendiente" de la ecuación de una línea recta es:
y − y1 = m(x − x1)
La ecuación es útil cuando sabemos:
y se quiere encontrar otros puntos en la línea.Primero juega con la animación (mueve el punto, prueba diferentes pendientes):
Ahora descubramos más.
¿Qué significa?
(x1, y1) es un punto conocido
m es la pendiente de la recta
(x, y) es cualquier otro punto en la línea
Dándole sentido
Se basa en la inclinación (pendiente):
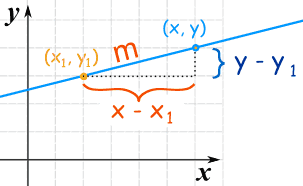
Pendiente m = cambio en y cambio en x = y − y1 x − x1
|
Empezamos con la pendiente: La reacomodamos así: Para obtener esto: |
 |
¡Entonces, es solo la fórmula de la pendiente de una manera diferente!
Ahora veamos cómo usarla.
Ejemplo 1:
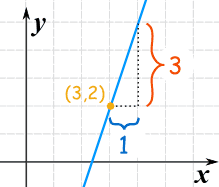
pendiente "m" = 31 = 3
y − y1 = m(x − x1)
Conocemos m y también tenemos el punto (x1, y1) = (3,2), por lo que:
y − 2 = 3(x − 3)
Ésa es una respuesta perfectamente buena, pero podemos simplificarla un poco:
y − 2 = 3x − 9
y = 3x − 9 + 2
y = 3x − 7
Ejemplo 2:
m = −3 1 = −3
y − y1 = m(x − x1)
Podemos elegir cualquier punto para (x1, y1), así que elijamos (0,0), y tenemos:
y − 0 = −3(x − 0)
Que se puede simplificar a:
y = −3x
Ejemplo 3: Línea Vertical
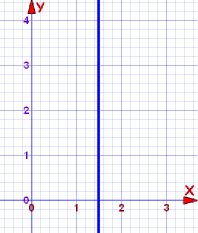 |
¿Cuál es la ecuación para una línea vertical?
¡La pendiente es indefinida!
De hecho, este es un caso especial, y usamos una ecuación diferente, como ésta:
x = 1.5
Cada punto en la línea tiene coordenada x igual
a 1.5,
por eso su ecuación es x = 1.5
¿Qué hay de y = mx + b ?
Es posible que ya estés familiarizado con la forma "y=mx+b" (llamada la forma pendiente-ordenada de la ecuación de una recta).
¡Es la misma ecuación, en una forma diferente!
El valor "b" (llamado la ordenada al origen) es donde la línea cruza el eje y.
Así que el punto (x1, y1) es en realidad (0, b)
y la ecuación se convierte en:
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

