Inversa de una Matriz usando Menores, Cofactores y la Adjunta
(Nota: también echa un vistazo a Matriz Inversa mediante operaciones de fila y la Calculadora de Matrices.)
Podemos calcular la Inversa de una Matriz así:
- Paso 1: calculando los Menores de la Matriz,
- Paso 2: luego convirtiéndolos en la Matriz de Cofactores,
- Paso 3: luego volviéndola Adjunta, y
- Paso 4: multiplicando eso por 1/Determinante.
¡Pero se explica mejor trabajando a través de un ejemplo!
Ejemplo: encuentra la inversa de A:
Necesita 4 pasos. Todo es simple aritmética, pero hay muchas operaciones, así que trata de no cometer un error.
Paso 1: Menores de la matriz
El primer paso es crear los "Menores de la Matriz". (Nota: también se conoce como "Matriz de Menores"). Este paso tiene la mayoría de los cálculos.Para cada elemento de la matriz:
- ignora los valores en la fila y columna en la que te encuentras
- calcula el determinante de los valores restantes
Pon esos determinantes en una matriz (los "Menores de la Matriz")
Determinante
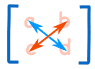
Para una matriz de 2×2 (2 filas y 2 columnas) el determinante es fácil: ad-bc
|
Piensa en una cruz diagonal:
|
 |
(Se vuelve más difícil para una matriz de 3×3, etc.)
Los cálculos
Aquí están los dos primeros y últimos dos cálculos de la "Matriz de Menores" (observa cómo ignoro los valores en la fila y las columnas actuales, y calculo el determinante usando los valores restantes):
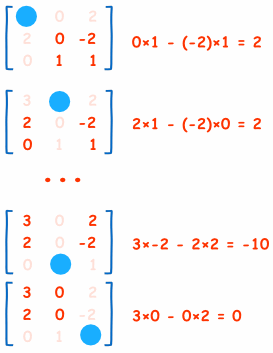
Y aquí está el cálculo para toda la matriz:
Paso 2: matriz de cofactores
¡Esto es fácil! Simplemente aplica un "tablero" de signos a los "Menores de la Matriz". En otras palabras, necesitamos cambiar el signo de las celdas alternantes, así:
Paso 3: Adjunta
Ahora "Transpón" todos los elementos de la matriz anterior ... en otras palabras, intercambia sus posiciones sobre la diagonal (la diagonal permanece igual):
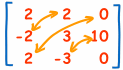
Paso 4: Multiplica por 1/determinante
Ahora calcula el determinante de la matriz original. Esto no es demasiado difícil, porque ya calculamos los determinantes de las partes más pequeñas cuando hicimos los "Menores de la Matriz".
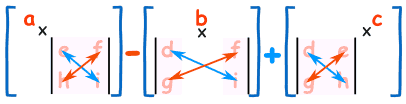
En la práctica, podemos multiplicar cada uno de los elementos de la fila superior por el cofactor para la misma ubicación:
Elementos de la fila superior: 3, 0, 2
Cofactores de la fila superior: 2, −2, 2
Determinante = 3×2 + 0×(−2) + 2×2 = 10
(Solo por diversión: intenta esto para cualquier otra fila o columna, también deberías obtener 10.)Y ahora multiplica la adjunta por 1/determinante:
¡Y listo!
Compara esta respuesta con la que obtuvimos en Matriz Inversa mediante operaciones de fila. ¿Es lo mismo? ¿Qué método prefieres?
Matrices más grandes
Son exactamente los mismos pasos para matrices más grandes (como una 4×4, 5×5, etc.), pero ¡wow! Hay muchos cálculos involucrados.Para una Matriz 4×4 tenemos que calcular 16 determinantes 3×3. Por lo tanto, a menudo es más fácil usar computadoras o calculadoras (como la Calculadora de Matrices.)
Conclusión
- Para cada elemento, calcula el determinante de los valores que no están en la fila o columna, para hacer la Matriz de Menores
- Aplica un tablero de signos para obtener la Matriz de Cofactores
- Transpón para obtener la Adjunta
- Multiplica por 1/Determinante para obtener la Inversa
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
