Determinante de una Matriz
El determinante de una matriz es un número especial que se puede calcular a partir de una matriz cuadrada.
Una matriz es un arreglo de números:
Una Matriz
(Ésta tiene 2 filas y 2 columnas)
El determinante de esa matriz es (los cálculos se explican más adelante):
¿Para qué sirve?
El determinante nos dice cosas sobre la matriz que son útiles en sistemas de ecuaciones lineales, nos ayuda a encontrar la matriz inversa, tiene aplicaciones en cálculo, etc.
Símbolo
El símbolo para determinante consiste en dos líneas verticales a cada lado.
Ejemplo:
|A| significa el determinante de la matriz A
(Exactamente el mismo símbolo que el valor absoluto.)
Cálculo del determinante
En primer lugar, la matriz debe ser cuadrada (es decir, tener el mismo número de filas que columnas). Luego es solo aritmética básica. Aquí se muestra cómo:
Para una matriz 2×2
Para una matriz de 2 × 2 (2 filas y 2 columnas):
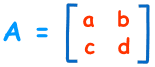
El determinante es:
|A| = ad − bc
"El determinante de A es igual a a por d menos b
por c"
|
Es fácil recordar cuando piensas en una cruz:
|
 |
Ejemplo:
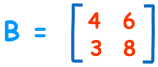
Para una matriz 3×3
Para una matriz de 3 × 3 (3 filas y 3 columnas):
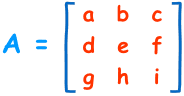
El determinante es:
|A| = a(ei − fh) − b(di − fg) +
c(dh − eg)
"El determinante de A es igual a ... etc."
Puede parecer complicado, pero hay un patrón:
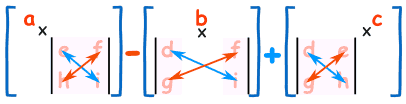
Para calcular el determinante de una matriz 3×3:
- Multiplica a por el determinante de la matriz 2×2 que no está en la fila o columna de a.
- Asimismo para b y para c
- Súmalos, pero recuerda el signo menos delante de la b
Como fórmula (recuerda que las barras verticales || significan "determinante de"):
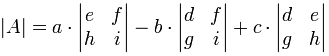
"El determinante de A es igual a a por el determinante de ...
etc."
Ejemplo:
Para matrices de 4×4 en adelante
El patrón continúa para matrices 4×4:
- más a por el determinante de la matriz que no está en la fila o columna de a,
- menos b por el determinante de la matriz que no está en la fila o columna de b,
- más c por el determinante de la matriz que no está en la fila o columna de c,
- menos d por el determinante de la matriz que no está en la fila o columna de d,

Como fórmula:
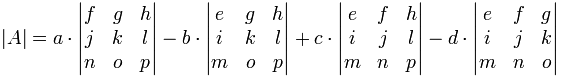
Observa el patrón +−+− (+a... −b... +c... −d...). Esto es importante para recordar.
El patrón continúa para matrices de 5×5 y superiores. Por lo general, ¡es mejor usar una Calculadora de Matrices para ésas!
No es el único camino
Este método de cálculo se llama "Expansión de Laplace" y me gusta porque el patrón es fácil de recordar. Pero hay otros métodos (solo para que lo sepas).
Resumen
- Para una matriz de 2×2 el determinante es ad - bc
- Para una matriz de 3×3 multiplica a por el determinante de la matriz 2×2 que no está en la columna ni fila de a, similarmente para b y c, ¡pero recuerda que b lleva delante un signo negativo!
- El patrón continúa para matrices más grandes: multiplica a por el determinante de la matriz que no está en la columna ni fila de a, continúa así para toda la fila y recuerda el patrón + − + −
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
