Sistemas de Ecuaciones Lineales
Una Ecuación Lineal es una ecuación
para una recta.
Una ecuación lineal no siempre tiene la forma y = 3.5 − 0.5x,
También puede ser escrita como y = 0.5(7 − x)
O como y + 0.5x = 3.5
O como y + 0.5x − 3.5 = 0 y más.
(Nota: ¡todas son la misma ecuación lineal!)
Un sistema de ecuaciones lineales es cuando tenemos dos o más ecuaciones lineales trabajando juntas.
Ejemplo: Aquí hay dos ecuaciones lineales:
| 2x | + | y | = | 5 |
| −x | + | y | = | 2 |
¿Puedes descubrir los valores de x y y tú mismo? (Solo inténtalo, juega un poco con ellas).
Intentemos construir y resolver un ejemplo del mundo real:
Ejemplo: Tú contra un caballo

Puedes correr 0.2km por minuto.
El caballo puede correr 0.5km por minuto. Pero lleva 6 minutos ensillar al caballo.
¿Hasta dónde puedes llegar antes de que el caballo te alcance?
Podemos hacer dos ecuaciones (d = distancia en km, t = tiempo en minutos)
- Corres a 0.2 km por minuto, así que d = 0.2t
- El caballo corre a 0.5 km por minuto, pero le quitamos 6 min de su tiempo: d = 0.5(t−6)
Entonces tenemos un sistema de ecuaciones (que son lineales):
- d = 0.2t
- d = 0.5(t−6)
La podemos resolver en una gráfica:
Parece que te alcanza después de 10 minutos ... solo después de 2 km de distancia.
Corre más rápido la próxima vez.
Entonces ahora sabes lo que es un Sistema de Ecuaciones Lineales.
Sigamos descubriendo más sobre ellos ...
Resolver
¡Puede haber muchas formas de resolver ecuaciones lineales!
Veamos otro ejemplo:
Ejemplo: Resuelve estas dos ecuaciones:
- x + y = 6
- −3x + y = 2
Bueno, podemos ver dónde se cruzan, por lo que ya está resuelto gráficamente.
¡Pero ahora vamos a resolverlo usando Álgebra!
Hmmm ... ¿cómo resolver esto? ¡Puede haber muchas formas! En este caso, ambas ecuaciones tienen "y", así que intentemos restar toda la segunda ecuación de la primera:
Ahora simplifiquémoslo:
Y podemos encontrar el valor correspondiente de y usando cualquiera de las dos ecuaciones originales (porque sabemos que tienen el mismo valor en x = 1). Usemos la primera (puedes probar el segundo tú mismo):
Y la solución es:
x = 1 y y = 5
¡Y la gráfica nos muestra que tenemos razón!
Ecuaciones lineales
Solo se permiten variables simples en ecuaciones lineales. No x2, y3, √x, etc:
Lineal vs no-lineal
Dimensiones
| Una Ecuación Lineal puede tener 2 dimensiones ... (tales como x y y) |
 |
|
| ... o 3 dimensiones ... (forma un plano) |
 |
|
| ... o 4 dimensiones ... | ||
| ... ¡o más! |
Variables Comunes
Para que las ecuaciones "trabajen juntas" tienen que compartir una o más variables:
Un sistema de ecuaciones tiene dos o más ecuaciones en una o más variables
Más Variables
Entonces, un Sistema de Ecuaciones podría tener muchas ecuaciones y muchas variables.
Ejemplo: 3 ecuaciones con 3 variables
| 2x | + | y | − | 2z | = | 3 |
| x | − | y | − | z | = | 0 |
| x | + | y | + | 3z | = | 12 |
- 2 ecuaciones en 3 variables,
- 6 ecuaciones en 4 variables,
- 9,000 ecuaciones en 567 variables,
- etc.
Soluciones
Cuando el número de ecuaciones es el mismo que el número de variables, es probable que haya una solución. No garantizado, pero probable.
De hecho, solo hay tres casos posibles:
- No hay solución
- Una solución
- Infinitas soluciones
Si hay una o infinitas soluciones se llaman "consistentes".
Aquí hay un diagrama para 2 ecuaciones en 2 variables:
Independiente
De lo contrario, son "dependientes".
También se llama "independencia lineal" y "dependencia lineal"
Ejemplo:
- x + y = 3
- 2x + 2y = 6
Entonces la segunda ecuación no dio nueva información.
Donde las ecuaciones son verdaderas
El truco es encontrar dónde todas las ecuaciones son se cumplen al mismo tiempo.¿Cumplirse? Qué significa eso?
Nota: cuando una ecuación se cumple a veces también se dice que es verdadera.
Ejemplo: Tú contra un caballo
En cualquier lugar de esa línea d es igual a 0.2t
- en t=5 y d=1, la ecuación es verdadera (¿Está en d = 0.2t? Sí, ya que 1 = 0.2×5 es verdad)
- en t=5 y d=3, la ecuación no es verdadera(¿Está en d = 0.2t? No, ya que 3 = 0.2×5 no es verdad)
De la misma manera, la línea que representa al caballo es verdadera en toda su longitud (pero en ninguna otra parte).
Pero solo en el punto donde se cruzan (en t = 10, d = 2) son ambas verdaderas.
... por eso algunas personas los llaman "Ecuaciones lineales simultáneas"
Resolver usando álgebra
Es frecuente utilizar Álgebra para resolverlos.
Aquí está el ejemplo del caballo resuelto usando Álgebra:
Ejemplo: Tú contra un caballo
El sistema de ecuaciones es:
- d = 0.2t
- d = 0.5(t−6)
En este caso, parece más fácil establecerlos iguales entre sí:
d = 0.2t = 0.5(t−6)
¡Ahora sabemos cuándo te alcanza!
Y nuestra solución es:
t = 10 minutos y d = 2 km
Álgebra vs Gráficas
¿Por qué usar Álgebra cuando las gráficas son tan fáciles? Porque:
Más de 2 variables no se pueden resolver con una gráfica simple.
Entonces el Álgebra viene al rescate con dos métodos populares:- Resolver por sustitución
- Resolver por eliminación
Resolver por sustitución
Estos son los pasos:
- Escribe una de las ecuaciones para que esté en el estilo "variable = ..."
- Reemplaza (i.e., sustituye) esa variable en la otra ecuación (o ecuaciones).
- Resuelve la otra ecuación (o ecuaciones)
- (Repite según sea necesario)
Aquí hay un ejemplo con 2 ecuaciones en 2 variables:
Ejemplo:
- 3x + 2y = 19
- x + y = 8
Usemos la segunda ecuación y la variable "y" (parece la ecuación más simple).
Escribe una de las ecuaciones para que tenga el estilo "variable = ...":
Podemos restar x de ambos lados de x + y = 8 para obtener y = 8 − x. Ahora nuestras ecuaciones se ven así:
- 3x + 2y = 19
- y = 8 − x
Ahora reemplaza "y" con "8 − x" en la otra ecuación:
- 3x + 2(8 − x) = 19
- y = 8 − x
Resuelve usando los métodos habituales de álgebra:
Desarrolla 2(8−x):
- 3x + 16 − 2x = 19
- y = 8 − x
Luego 3x−2x = x:
- x + 16 = 19
- y = 8 − x
Y finalmente 19−16=3
- x = 3
- y = 8 − x
Ahora que sabemos el valor de x, podemos ponerlo en la ecuación y = 8 − x:
- x = 3
- y = 8 − 3 = 5
Y la respuesta es:
x = 3
y = 5
Nota: debido a que hay una solución, las ecuaciones son "consistentes"
Comprobación: ¿por qué no verificas si x = 3 y y = 5 se cumplen en ambas ecuaciones?
Resolver por sustitución: 3 ecuaciones en 3 variables
¡Okay! Pasemos a un ejemplo más largo: 3 ecuaciones en 3 variables.Ejemplo:
- x + z = 6
- z − 3y = 7
- 2x + y + 3z = 15
Deberíamos alinear las variables ordenadamente, o podemos perder la noción de lo que estamos haciendo:
| x | + | z | = | 6 | |||||
| − | 3y | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 |
Podemos comenzar con cualquier ecuación y cualquier variable. Usemos la primera ecuación y la variable "x".
Escribe una de las ecuaciones para que tenga el estilo "variable = ...":
| x | = | 6 − z | |||||||
| − | 3y | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 | |||
Ahora reemplaza "x" con "6 − z" en las otras ecuaciones:
(Afortunadamente, solo hay otra ecuación con x)
| x | = | 6 − z | ||||||||
| − | 3y | + | z | = | 7 | |||||
| 2(6−z) | + | y | + | 3z | = | 15 | ||||
Resuelve usando los métodos habituales de álgebra:
2(6−z) + y + 3z = 15 se simplifica a y + z = 3:
| x | = | 6 − z | |||||||
| − | 3y | + | z | = | 7 | ||||
| y | + | z | = | 3 | |||||
Bien. Hemos progresado un poco, pero todavía nos falta.
Ahora repite el proceso, pero solo para las últimas 2 ecuaciones.
Escribe una de las ecuaciones para que tenga el estilo "variable = ...":
Elige la última ecuación y la variable z:
| x | = | 6 − z | |||||||
| − | 3y | + | z | = | 7 | ||||
| z | = | 3 − y | |||||||
Ahora reemplaza "z" con "3 − y" en la otra ecuación:
| x | = | 6 − z | |||||||
| − | 3y | + | 3 − y | = | 7 | ||||
| z | = | 3 − y | |||||||
Resuelve usando los métodos habituales de álgebra:
−3y + (3−y) = 7 se simplifica a −4y = 4, o en otras palabras y = −1
| x | = | 6 − z | |||||||
| y | = | −1 | |||||||
| z | = | 3 − y | |||||||
¡Casi listo!
Sabiendo que y = −1 podemos calcular z = 3−y = 4:
| x | = | 6 − z | |||||||
| y | = | −1 | |||||||
| z | = | 4 | |||||||
Y sabiendo que z = 4 podemos calcular que x = 6−z = 2:
| x | = | 2 | |||||||
| y | = | −1 | |||||||
| z | = | 4 |
Y la respuesta es:
x = 2
y = −1
z = 4
Comprobación: por favor verifica esto tú mismo.
Podemos usar este método para 4 o más ecuaciones y variables ... simplemente haz los mismos pasos una y otra vez hasta que se resuelva.
Conclusión: la sustitución funciona bien, pero lleva mucho tiempo hacerla.
Resolver por eliminación
La eliminación puede ser más rápida ... pero debe mantenerse ordenada.
"Eliminar" significa remover: este método funciona eliminando variables hasta que solo quede una.
- multiplicar una ecuación por una constante (excepto cero),
- sumar (o restar) una ecuación a otra ecuación
¿POR QUÉ podemos sumar ecuaciones entre sí?
Imagina dos ecuaciones realmente simples:
x − 5 = 3
5 = 5
Podemos sumar "5 = 5" a "x − 5 = 3":
x − 5 + 5 = 3 +
5
x = 8
Funcionará bien, porque ambos lados son iguales (para eso está el signo =)
OK, es hora de un ejemplo completo. Usemos las 2 ecuaciones de 2 variables del ejemplo de antes:
Ejemplo:
- 3x + 2y = 19
- x + y = 8
Muy importante para mantener las cosas ordenadas:
| 3x | + | 2y | = | 19 | |||
| x | + | y | = | 8 |
Ahora ... nuestro objetivo es eliminar una variable de una ecuación.
Primero vemos que hay un "2y" y una "y", así que trabajemos en eso.Multipliquemos la segunda ecuación por 2:
| 3x | + | 2y | = | 19 | |||
| 2x | + | 2y | = | 16 |
Restemos la segunda ecuación de la primera ecuación:
| x | = | 3 | |||||
| 2x | + | 2y | = | 16 |
¡Hurra! ¡Ahora sabemos cuánto es x!
A continuación, vemos que la segunda ecuación tiene "2x", así que dividamos a la mitad y luego restemos "x":Multipliquemos la segunda ecuación por ½ (es decir, dividir por 2):
| x | = | 3 | |||||
| x | + | y | = | 8 |
Restemos la primera ecuación de la segunda ecuación:
| x | = | 3 | |||||
| y | = | 5 |
Y la respuesta es:
x = 3 y y = 5
Y aquí está la gráfica:
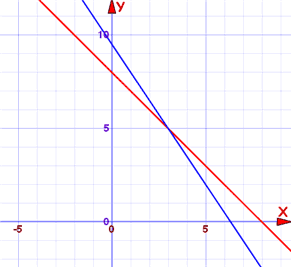
La línea azul es donde 3x + 2y = 19 se cumple
La línea roja es donde x + y = 8 se cumple
En x = 3, y = 5 (donde se cruzan las líneas) ambas se cumplen. Ésa es la respuesta.
Aquí hay otro ejemplo:
Ejemplo:
- 2x − y = 4
- 6x − 3y = 3
Pongamos todo ordenadamente:
| 2x | − | y | = | 4 | |||
| 6x | − | 3y | = | 3 |
Multipliquemos la primera ecuación por 3:
| 6x | − | 3y | = | 12 | |||
| 6x | − | 3y | = | 3 |
Restemos la segunda ecuación de la primera:
| 0 | − | 0 | = | 9 | |||
| 6x | − | 3y | = | 3 |
0 − 0 = 9 ???
¿Qué está pasando aquí?
En pocas palabras, no hay solución.
| En realidad son líneas paralelas: |
Y por último:
Ejemplo:
- 2x − y = 4
- 6x − 3y = 12
Ordenamos:
| 2x | − | y | = | 4 | |||
| 6x | − | 3y | = | 12 |
Multiplicamos la primera ecuación por 3:
| 6x | − | 3y | = | 12 | |||
| 6x | − | 3y | = | 12 |
Restamos la segunda ecuación de la primera:
| 0 | − | 0 | = | 0 | |||
| 6x | − | 3y | = | 3 |
0 − 0 = 0
Bueno, ¡eso es realmente VERDADERO! Cero es igual a cero ...
... eso es porque son realmente la misma ecuación ...
... así que hay un número infinito de soluciones
| Son la misma línea: |
Y ahora hemos visto un ejemplo de cada uno de los tres casos posibles:
- No hay solución
- Una solución
- Infinitas soluciones
Resolviendo por eliminación: 3 ecuaciones en 3 variables
Antes de comenzar con el siguiente ejemplo, veamos una forma mejorada de hacer las cosas.
Si seguimos este método es menos probable que cometamos un error.
- Eliminamos las xs primero (de la ecuación 2 y 3, en orden)
- luego eliminamos y (de la ecuación 3)
Entonces tenemos esta "forma triangular":
Ahora comenzamos en la parte inferior y trabajamos
de nuevo hacia arriba
(ponemos z para encontrar y, luego z
y y para encontrar x):
Y lo tenemos solucionado:
TAMBIÉN, encontraremos que es más fácil hacer algunos de los cálculos en la cabeza, o en un pedacito papel, en lugar de trabajar siempre dentro del conjunto de ecuaciones:
Ejemplo:
- x + y + z = 6
- 2y + 5z = −4
- 2x + 5y − z = 27
Escrito de forma ordenada:
| x | + | y | + | z | = | 6 | |||
| 2y | + | 5z | = | −4 | |||||
| 2x | + | 5y | − | z | = | 27 |
Primero, eliminamos x de la segunda y tercera ecuación.
No hay x en la segunda ecuación ... pasamos a la tercera ecuación:Restamos 2 veces la 1ra ecuación de la 3ra ecuación (solo hacemos esto en la cabeza o en papel):
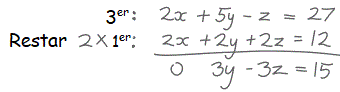
Y obtenemos:
| x | + | y | + | z | = | 6 | |||
| 2y | + | 5z | = | −4 | |||||
| 3y | − | 3z | = | 15 |
Luego, eliminamos y de la 3a ecuación.
Podríamos restar 1½ veces la segunda ecuación de la tercera ecuación (porque 1½ por 2 es 3) ...... pero podemos evitar fracciones si:
- multiplicamos la 3a ecuación por 2 y
- multiplicamos la 2da ecuación por 3
y luego hacemos la resta ... así:
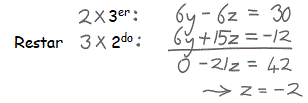
Y terminamos con:
| x | + | y | + | z | = | 6 | |||
| 2y | + | 5z | = | −4 | |||||
| z | = | −2 |
¡Ahora tenemos esa "forma de triángulo"!
Ahora vamos de vuelta "sustituyendo hacia atrás":
Conocemos el valor de z, así que 2y+5z=−4 se convierte en 2y−10=−4, luego 2y=6, por lo que y=3:
| x | + | y | + | z | = | 6 | |||
| y | = | 3 | |||||||
| z | = | −2 |
Después x+y+z=6 se convierte en x+3−2=6, de modo que x=6−3+2=5
| x | = | 5 | |||||||
| y | = | 3 | |||||||
| z | = | −2 |
Y la respuesta es:
x = 5
y = 3
z = −2
Comprobación: por favor verifica tú mismo :)
Consejos generales
Una vez que te acostumbras al Método de Eliminación, es más fácil que la Sustitución, porque solo sigues los pasos y aparecen las respuestas.Pero a veces la sustitución puede dar un resultado más rápido.
- La sustitución es a menudo más fácil para casos pequeños (como 2 ecuaciones o, a veces, 3 ecuaciones)
- La eliminación es más fácil para casos más grandes.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
