Ecuaciones Lineales

Una ecuación lineal es una ecuación para una línea recta

Estas son todas las ecuaciones lineales:

		y = 2x + 1
		5x = 6 + 3y
		y/2 = 3 − x

Veamos más de cerca un ejemplo:

Ejemplo: y = 2x + 1 es una ecuación lineal:

gráfica de una línea

La gráfica de y = 2x+1 es una línea recta

Cuando x aumenta, y aumenta el doble de rápido, por lo que necesitamos 2x
Cuando x es 0, y es 1. Así que necesitamos poner +1
De esta manera: y = 2x + 1

Aquí hay algunos valores de ejemplo:

x	y = 2x + 1
-1	y = 2 × (-1) + 1 = -1
0	y = 2 × 0 + 1 = 1
1	y = 2 × 1 + 1 = 3
2	y = 2 × 2 + 1 = 5

¡Comprueba tú mismo que esos puntos son parte de la línea de arriba!

Formas diferentes

Hay muchas formas de escribir ecuaciones lineales, pero la idea clave es:

Las variables solo están elevadas a la primera potencia (x, y, etc.),
Las variables no se multiplican entre sí (nada de xy),
No hay variables en los denominadores (nada de 1x, etc.)

Ejemplos: estas son ecuaciones lineales:

		y = 3x − 6
		y − 2 = 3(x + 1)
		y + 2x − 2 = 0
		5x = 6
		y/2 = 3

Pero las variables (como "x" o "y") en ecuaciones lineales NO tienen:

Exponentes (como el 2 en x²)
Raíces cuadradas, raíces cúbicas, etc

Ejemplos: estas NO son ecuaciones lineales:

		y² − 2 = 0
		3√x − y = 6
		x³/2 = 16
		xy = 1

Forma pendiente-ordenada

La forma más común es la de la ecuación de la recta pendiente-ordenada:

gráfica y=mx+b


Pendiente (Gradiente)	Ordenada a origen (intersección con el eje y)

Ejemplo: y = 2x + 1

Pendiente: m = 2
Ordenada: b = 1

¡Juega!

Puedes ver el efecto de diferentes valores
de m y b en Explora la gráfica de una línea recta

Forma punto-pendiente

Otra que es muy común es la Forma Punto-Pendiente de la ecuación de la línea recta:

y − y₁ = m(x − x₁)

Point-Slope Form

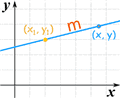Ejemplo: y − 3 = (¼)(x − 2)

Está en la forma y − y₁ = m(x − x₁) donde:

y₁ = 3
m = ¼
x₁ = 2

Forma general

Y también está la Forma General de la ecuación de la línea recta:

Ax + By + C = 0

(A y B no pueden ser ambos 0)

Ejemplo: 3x + 2y − 4 = 0

Está en la forma Ax + By + C = 0 donde:

A = 3
B = 2
C = −4

Hay otras formas menos comunes también.

Como función

A veces una ecuación lineal se escribe como una función, con f(x) en lugar de y:

y = 2x − 3

f(x) = 2x − 3

¡Son lo mismo!

Y las funciones no siempre se escriben usando f(x):

y = 2x − 3

w(u) = 2u − 3

h(z) = 2z − 3

¡También son lo mismo!

La función identidad

Hay una función lineal especial llamada "Función identidad":

f(x) = x

Y aquí está su gráfica:

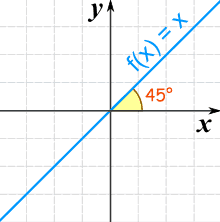
Función Identidad
Hace un ángulo de 45° (su pendiente es 1)

Se llama "Identidad" porque lo que sale es idéntico a lo que entra:

Entra	Sale
0	0
5	5
−2	−2
...etc.	...etc.

Funciones constantes

Otro tipo especial de función lineal es la Función Constante ... es una línea horizontal:

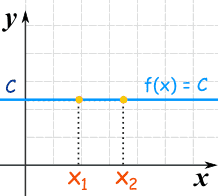
Función Constante

f(x) = C

No importa cuál sea el valor de "x", f(x) será siempre igual a algún valor constante.

Uso de Ecuaciones Lineales

Es posible que desees leer algunas de las cosas que se pueden hacer con las rectas:

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).