Rectas Paralelas y Rectas Perpendiculares
En esta página usaremos Álgebra para hallar rectas paralelas y perpendiculares.
Líneas paralelas
¿Cómo sabemos cuando dos líneas son paralelas?
¡Sus pendientes son iguales!
|
La pendiente es el valor m en la ecuación de la recta: y = mx + b |
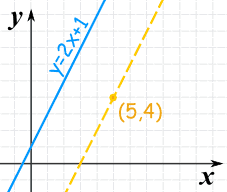
Ejemplo:
Encuentra la ecuación de la línea que es:
- paralela a y = 2x + 1
- y que pasa por el punto (5,4)
La pendiente de y=2x+1 es: 2
La línea paralela debe tener la misma pendiente de 2.
Podemos encontrarla usando la ecuación de la recta "punto-pendiente":
y − y1 = 2(x − x1)
Y luego poner el punto (5,4):
y − 4 = 2(x − 5)
Y esa respuesta está bien, pero también pongámosla en la forma y = mx + b:
y − 4 = 2x − 10
y = 2x − 6
Líneas verticales
Pero esto no funciona para líneas verticales ... Te explico porqué al final.
No es la misma línea
¡Ten cuidado! Pueden ser la misma línea (pero con una ecuación
diferente), por lo que no son paralelas.
¿Cómo sabemos si realmente son la misma línea? Verifica sus
intersecciones en el eje y (la ordenada al origen) así como su
pendiente:
Ejemplo: ¿es y = 3x + 2 paralela a y − 2 = 3x?
Para y = 3x + 2: la pendiente es 3, y la ordenada al origen es 2
Para y − 2 = 3x: la pendiente es 3, y la ordenada al origen es 2
De hecho, son la misma línea por lo que no son paralelas
Líneas perpendiculares
Dos líneas son perpendiculares cuando se encuentran en ángulo recto (90°).Para encontrar una pendiente perpendicular:
Cuando una línea tiene pendiente m, una línea perpendicular tiene pendiente −1m
En otras palabras, es el recíproco negativo
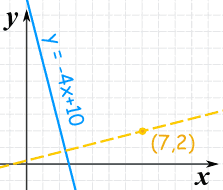
Ejemplo:
Encuentra la ecuación de la línea que es
- perpendicular a y = −4x + 10
- y que pasa por (7,2)
La pendiente de y=−4x+10 es: −4
El recíproco negativo de esa pendiente es:
m = −1−4 = 14
Entonces la línea perpendicular tendrá una pendiente de 1/4:
y − y1 = (1/4)(x − x1)
Y ahora sustituimos el punto (7,2):
y − 2 = (1/4)(x − 7)
Y esa respuesta está bien, pero también pongámosla en la forma "y = mx + b":
y − 2 = x/4 − 7/4
y = x/4 + 1/4
Comprobación rápida de perpendicularidad
Cuando multiplicamos una pendiente m por su pendiente perpendicular −1m se obtiene −1.
Entonces, para verificar rápidamente si dos líneas son perpendiculares:
Cuando multiplicamos sus pendientes, obtenemos −1
De esta forma:
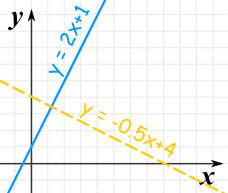
¿Son estas dos líneas perpendiculares?
| Línea | Pendiente |
| y = 2x + 1 | 2 |
| y = −0.5x + 4 | −0.5 |
Cuando multiplicamos las dos pendientes obtenemos:
2 × (−0.5) = −1
Sí, tenemos −1, por lo que son perpendiculares.
Líneas verticales
Los métodos anteriores funcionan bien, excepto para líneas verticales:
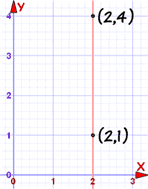
En este caso el gradiente no está definido (puesto que no podemos dividir entre 0):
m = yA − yBxA − xB = 4 − 12 − 2 = 30 = indefinido
Tan solo confía en el hecho de que:
- una línea vertical es paralela a otra línea vertical.
- una línea vertical es perpendicular a una línea horizontal (y viceversa).
Resumen
- líneas paralelas: misma pendiente
- líneas perpendiculares: la pendiente es el recíproco negativo (−1/m)
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
