Inversa de una Matriz
Por favor lee primero nuestra Introducción a las Matrices.
¿Cuál es la inversa de una matriz?
Éste es el recíproco de un número:
Reciprocal of a Number
La inversa de una matriz es la misma idea pero la escribimos A-1
¿Por qué no 1/A ? ¡Porque no dividimos por una matriz! Y de todas formas 1/8 también se puede escribir como 8-1
Y hay otras similitudes:
Cuando multiplicamos un número por su recíproco obtenemos 1
Cuando multiplicamos una matriz por su inversa, obtenemos la Matriz Identidad (que es como "1" para las matrices):
Lo mismo cuando lo inverso viene primero:
Matriz Identidad
Acabamos de mencionar la "Matriz Identidad". Es el equivalente matricial del número "1":
Una matriz identidad de 3x3
- Es "cuadrada" (tiene el mismo número de filas que columnas),
- Tiene 1s en diagonal y 0s en cualquier otro lugar.
- Su símbolo es la letra mayúscula I.
Definición
Aquí está la definición:
La inversa de A es A-1 solo cuando:
A × A-1 = A-1 × A = I
A veces no hay inversa en absoluto.
Matriz 2x2
OK, ¿cómo calculamos la inversa?Bueno, para una matriz de 2x2 la inversa es:
En otras palabras: intercambia las posiciones de a y d, coloca signos negativos frente a b y c, y divide todo por determinante (ad-bc).
Probemos un ejemplo:
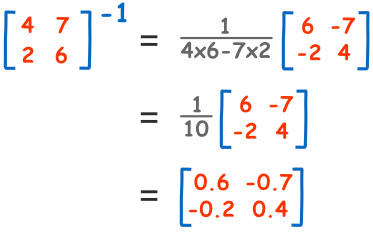
¿Cómo sabemos que ésta es la respuesta correcta?
Recuerda que debe ser cierto que: A × A-1 = I
Entonces, verifiquemos qué sucede cuando multiplicamos la matriz por su inversa:
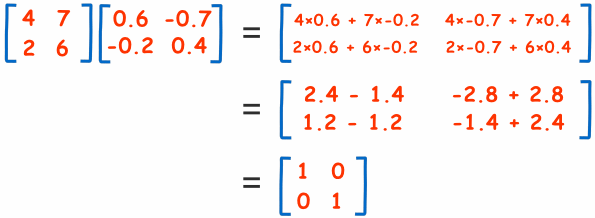
Y, ¡hey, terminamos con la Matriz Identidad! Entonces debe ser correcta.
También debe ser verdad que: A-1 × A = I
¿Por qué no intentas multiplicarlos? Verifica que también obtienes la Matriz Identidad:

¿Por qué necesitamos una inversa?
¡Porque con las matrices no dividimos! En serio, no existe el concepto de dividir por una matriz.Pero podemos multiplicar por una inversa, que logra lo mismo.
Imagina que no podemos dividir entre números ...
... y alguien pregunta "¿Cómo comparto 10 manzanas con 2 personas?"Pero podemos tomar el recíproco de 2 (que es 0.5), entonces respondemos:
10 × 0.5 = 5
Obtienen 5 manzanas cada uno.
Lo mismo se puede hacer con las matrices:
Digamos que queremos encontrar la matriz X, y que conocemos las matrices A y B:
XA = B
Sería bueno dividir ambos lados por A (para obtener X=B/A), pero recuerda que no podemos dividir.
Pero, ¿y si multiplicamos ambos lados por A-1 ?
XAA-1 = BA-1
Y sabemos que AA-1 = I, por lo tanto:
XI = BA-1
Podemos eliminar I (por la misma razón que podemos eliminar "1" de 1x = ab para los números):
X = BA-1
Y tenemos nuestra respuesta (suponiendo que podamos calcular A-1)
En ese ejemplo, tuvimos mucho cuidado de hacer las multiplicaciones correctas, porque con las matrices el orden de multiplicación es importante. AB casi nunca es igual a BA.
Un ejemplo de la vida real: camión y tren

Tomaron el tren de regreso a $3.50 por niño y $3.60 por adulto para un total de $135.20.
¿Cuántos niños y cuántos adultos viajaron?
Primero, configuremos las matrices (¡ten cuidado de que las filas y columnas sean correctas!):
Esto es como el ejemplo anterior:
XA = B
Así que para resolverlo necesitamos la inversa de "A":
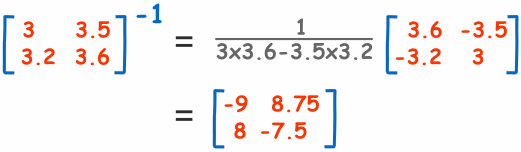
Ahora que tenemos la inversa, podemos resolver usando:
X = BA-1

La respuesta casi parece mágica. Pero se basa en buenas matemáticas.
Cálculos así (pero usando matrices mucho más grandes) ayudan a los
ingenieros a diseñar edificios, se usan en videojuegos y animaciones
por computadora para hacer que las cosas se vean tridimensionales y en
muchos otros lugares.
También es una forma de resolver Sistemas
de Ecuaciones Lineales.
Los cálculos se realizan por computadora, pero las personas deben entender las fórmulas.
El orden es importante
Digamos que estamos tratando de encontrar "X" en este caso:
AX = B
¡Esto es diferente al ejemplo anterior! La X ahora está después de A.
Con las matrices, el orden de multiplicación generalmente cambia la respuesta. No asumas que AB = BA, pues casi nunca es cierto.Entonces, ¿cómo resolvemos éste? Usando el mismo método, pero poniendo A-1 en frente:
A-1AX = A-1B
Y sabemos que A-1A= I, por lo tanto:
IX = A-1B
Podemos quitar I:
X = A-1B
Y tenemos nuestra respuesta (suponiendo que podamos calcular A-1)
Se puede hacer de esa manera, pero debemos tener cuidado de cómo configurarlo.
Así es como se ve AX = B:

¡Se ve tan ordenado! Creo que lo prefiero así.
Observa también cómo se intercambian las filas y
columnas
("Transpuesta") en comparación con el ejemplo anterior.
Para resolverlo necesitamos la inversa de "A":
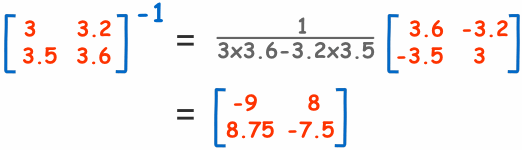
Es como la inversa que obtuvimos antes, pero
Transpuesta (filas y columnas intercambiadas).
Ahora podemos resolver usando:
X = A-1B
Por lo tanto, las matrices son cosas poderosas, ¡pero deben configurarse correctamente!
La inversa puede no existir
En primer lugar, para tener la inversa, la matriz debe ser "cuadrada" (el mismo número de filas y columnas).Pero también el determinante no puede ser cero (o terminamos dividiendo por cero). ¿Qué tal esto?
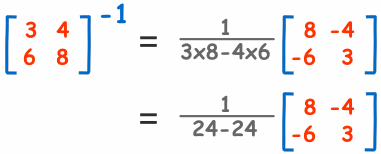
¿24-24? Eso es igual a 0, y 1/0 no está
definido.
¡No podemos ir más allá! Esta matriz no tiene inversa.
Tal matriz se llama "Singular", que solo ocurre cuando el determinante es cero.
Y tiene sentido ... mira los números: la segunda fila es el doble de la primera fila y no agrega ninguna información nueva.Y el determinante nos permite conocer este hecho.
(Imagina en nuestro ejemplo de camión y tren que los precios en el tren eran exactamente un 50% más altos que el camión: así que ahora no podemos encontrar diferencias entre adultos y niños. Es necesario que haya algo que los distinga).
Matrices más grandes
La inversa de una matriz 2x2 es fácil ... en comparación con matrices más grandes (como 3x3, 4x4, etc.).Para esas matrices más grandes hay tres métodos principales para hallar la inversa:
- Usando Operaciones Elementales en las Filas (Gauss-Jordan)
- Usando Menores, Cofactores, Adjuntas
- Usando una computadora (como la Calculadora de Matrices)
Conclusión
- La inversa de A es A-1 solo cuando A × A-1 = A-1 × A = I
- Para encontrar la inversa de una matriz de 2x2: intercambia las posiciones de a y d, coloca signos negativos frente a b y c, y divide todo por el determinante (ad−bc).
- A veces no hay inversa.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

