Cuadrados y Raíces Cuadradas en Álgebra
Puede que quieras leer primero la Introducción a los Cuadrados y a las Raíces Cuadradas.
Cuadrados
Para elevar al cuadrado un número, simplemente multiplícalo por sí mismo ...
Ejemplo: ¿Cuánto es 3 al cuadrado?
| 3 al cuadrado | = |  |
= 3 × 3 = 9 |
"Elevar al cuadrado" a menudo se escribe con un pequeño 2 como este:
Esto dice "4 al cuadrado es igual a 16"
(el pequeño 2 significa que el número aparece dos veces al
multiplicar, entonces 4×4=16)
Raíz cuadrada
Una raíz cuadrada va en la otra dirección:
3 al cuadrado es 9, entonces una raíz cuadrada de 9 es 3
Es como preguntar:
¿Qué puedo multiplicar por sí mismo para obtener esto?
Definición
Aquí tienes la definición:
La raíz cuadrada de x es un número r cuyo cuadrado es x:
r2 = x
El símbolo de la raíz cuadrada
Este es el símbolo especial que significa "raíz cuadrada", es como
una marca de verificación,
y de hecho comenzó hace cientos de años como un punto con un trazo
hacia arriba.
Se llama radical, ¡y siempre hace que las matemáticas
parezcan importantes!
Podemos usarlo así:
decimos "la raíz cuadrada de 9 es igual a 3"
Ejemplo: ¿Cuánto es √36?
Respuesta: 6 × 6 = 36, por lo que √36 = 6
Números negativos
Los números negativos también se pueden elevar al cuadrado.
Ejemplo: ¿Cuánto es menos 5 al cuadrado?
... pero... ¿qué significa "menos 5 al cuadrado"?
- ¿elevar el 5 al cuadrado y luego poner el menos?
- ¿o elevar (−5) al cuadrado?
¡No está claro! Y obtenemos respuestas diferentes:
- elevar el 5 al cuadrado, luego el menos: −(5×5) = −25
- elevar (−5) al cuadrado: (−5)×(−5) = +25
Así que vamos a aclararlo usando los paréntesis "( )".
Ejemplo corregido: ¿Cuánto es (−5)2?
Respuesta:
(−5) × (−5) = 25
(porque un negativo por un negativo da un positivo)
¡Eso fue interesante!
Cuando elevamos al cuadrado un número negativo obtenemos un resultado positivo.
Exactamente igual que cuando elevamos al cuadrado un número positivo:
Ahora, ¿recuerdas nuestra definición de raíz cuadrada?
La raíz cuadrada de x es un número r cuyo cuadrado es x:
r2 = x
Y acabamos de descubrir que:
(+5)2 = 25
(−5)2 = 25
Hay dos números cuyo cuadrado da 25.
Por lo tanto, tanto +5 como −5 son raíces cuadradas de 25.
Dos raíces cuadradas
¡Puede haber una raíz cuadrada positiva y una negativa!
Es importante recordar esto.
Ejemplo: Resuelve w2 = a
Respuesta:
w = √a y w = −√a
Raíz cuadrada principal
Si hay dos raíces cuadradas, ¿por qué decimos que √25 = 5?
El símbolo √ significa la raíz cuadrada principal (no negativa)
Existen dos raíces cuadradas, pero el símbolo √ se refiere solo a la raíz cuadrada principal.
Ejemplo:
Las raíces cuadradas de 36 son 6 y −6
Pero √36 = 6 (no −6)
La Raíz Cuadrada Principal a veces se llama Raíz Cuadrada Positiva (pero puede ser cero).
Signo Más-Menos
| ± | es un símbolo especial que significa "más o menos", |
| así que en lugar de escribir: | w = √a y w = −√a | |
| podemos escribir: | w = ±√a |
En pocas palabras
¿Por qué es esto importante?
¿Por qué es importante este "más o menos"? ¡Porque no queremos perder ninguna solución!
Ejemplo: Resuelve x2 − 9 = 0
El "±" nos indica que debemos incluir también el "−3" como respuesta.
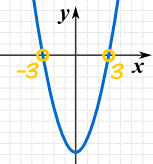
Ejemplo: Resuelve x en (x − 3)2 = 16
Comprobación: (7−3)2 = 42 = 16
Comprobación: (−1−3)2 = (−4)2 = 16
Raíz cuadrada de xy
Cuando dos números se multiplican dentro de una raíz cuadrada, podemos separarlos en una multiplicación de dos raíces cuadradas de esta forma:
√ = √√
pero solo cuando x e y son ambos mayores o iguales a 0
Ejemplo: ¿Cuánto es √(100×4)?
Y √√ = √:
Ejemplo: ¿Cuánto es √8√2?
Ejemplo: ¿Cuánto es √(−8 × −2)?
¡Parece que hemos caído en una trampa!
Podemos usar Números imaginarios, pero eso nos llevaría a una respuesta incorrecta de −4.
Ah, es cierto...
La regla solo funciona cuando x e y son ambos mayores o iguales a 0.
Así que no podemos usar esa regla aquí.
En su lugar, simplemente hazlo de esta manera:
√(−8 × −2) = √16 = +4
¿Por qué √ = √√?
Podemos usar el hecho de que elevar al cuadrado una raíz cuadrada nos devuelve el valor original:
(√)2 = a
¡Suponiendo que a no sea negativo!
Pero solo si tanto x como y son mayores o iguales a 0.
Un exponente de un medio
Una raíz cuadrada también se puede escribir como un exponente fraccionario de un medio:
√ = x½
pero solo para x mayor o igual a 0
¿Y la raíz cuadrada de negativos?
El resultado es un Número imaginario... lee esa página para aprender más.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
