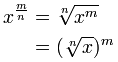Exponentes fraccionarios

También se llaman "radicales" o "exponentes racionales"

Exponentes enteros

Primero, veamos los exponentes con números enteros:

El exponente de un número dice cuántas veces se multiplica el número.

En este ejemplo: 8² = 8 × 8 = 64

En palabras: 8² se puede leer "8 a la segunda potencia", "8 a la potencia 2" o simplemente "8 al cuadrado"

Otro ejemplo: 5³ = 5 × 5 × 5 = 125

Exponentes fraccionarios:

¿Pero qué ocurre si el exponente es una fracción?

El exponente 12 es en realidad la raíz cuadrada

El exponente13 es la raíz cúbica

El exponente 14 es la raíz cuarta

¡Y así sucesivamente!

$exponente fraccionario: 4^(1/2) = raíz cuadrada de 4, etc.$

¿Por qué?

Veamos porqué mediante un ejemplo

Primero, la Ley de los exponentes nos dice cómo manejar los exponentes cuando multiplicamos:

Ejemplo: x²x² = (xx)(xx) = xxxx = x⁴

Lo cual nos muestra que x²x² = x⁽²⁺²⁾ = x⁴

Ahora intentemos lo mismo con exponentes fraccionarios:

Ejemplo: ¿Cuánto es 9^½ × 9^½ ?

9^½ × 9^½ = 9^(½+½) = 9⁽¹⁾ = 9

De modo que 9^½ multiplicado por sí mismo da 9.

¿Cómo se le llama a un número que, cuando se multiplica por sí mismo, nos da otro número? ¡La raíz cuadrada!

Observa:

√9 × √9 = 9

9^½ × 9^½ = 9

Por lo tanto 9^½ es lo mismo que √9

Probamos con otra fracción

Vamos a probar otra vez, pero con un exponente de un cuarto (1/4):

Ejemplo:

16^¼ × 16^¼ × 16^¼ × 16^¼ = 16^{(¼+¼+¼+¼)} = 16⁽¹⁾ = 16

Por lo que 16^¼ usado 4 veces en una multiplicación da 16,

en consecuencia 16^¼ es la raíz cuarta de 16

Regla general

Funcionó para ½, también con ¼, de hecho funciona en general:

x^1/n = La raíz n-ésima de x

Por lo que podemos establecer una regla general:

Un exponente fraccionario como 1/n significa calcular la raíz n-ésima:

Ejemplo: ¿Cuánto es 27^1/3 ?

Respuesta: 27^1/3 = 27 = 3

¿Qué pasa con fracciones más complicadas?

¿Qué tal un exponente fraccionario como 4^3/2?

En realidad está diciendo, eleva al cubo (3) y saca la raíz cuadrada (1/2), sin importar el orden.

Permíteme explicarlo.

Las fracciones (como m/n) se pueden separar en dos partes:

una parte con un número entero (m), y
una parte con una fracción del tipo 1/n

Así, dado que m/n = m × (1/n), podemos hacer lo siguiente:

El orden no importa, por lo que también funciona para m/n = (1/n) × m:

Así que tenemos esto:

Un exponente fraccionario como m/n significa:

Calcula la potencia m-ésima, después haz la raíz n-ésima

O calcula la raíz n-ésima y después eleva a la potencia m-ésima

Algunos ejemplos:

Ejemplo: ¿Cuánto es 4^3/2 ?

4^3/2 = 4^3×(1/2) = √(4³) = √(4×4×4) = √(64) = 8

4^3/2 = 4^(1/2)×3 = (√4)³ = (2)³ = 8

De ambas formas se obtiene el mismo resultado.

Ejemplo: ¿Cuánto es 27^4/3 ?

27^4/3 = 27^4×(1/3) = (27⁴) = (531441) = 81

27^4/3 = 27^(1/3)×4 = (27)⁴ = (3)⁴ = 81

¡En este caso fue mucho más sencillo de la segunda manera!

Ahora... ¡Juega con el gráfico!

Mira cómo la curva cambia suavemente cuando juegas con las fracciones en esta animación, esto te indica que la idea de exponentes fraccionarios funciona bien.

Cosas que probar:

Empieza con m=1 y n=1, después aumenta la n poco a poco para que veas 1/2, 1/3 y 1/4
Después prueba m=2 y mueve la n para ver fracciones como 2/3, etc.
Ahora haz que el exponente sea −1
Finalmente prueba a hacer m más grande, después n más pequeño, después m más pequeño, después n más grande: la curva debería dar vueltas.

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).