Serie de Taylor
Una Serie de Taylor es un desarrollo (o expansión) de una función en una suma infinita de términos, donde el exponente de cada término es cada vez mayor, así:
Ejemplo: La Serie de Taylor para ex
ex = 1 + x + x22! + x33! + x44! + x55! + ...
(Nota: ! es la Función Factorial)
¿Realmente funciona?
Usando una calculadora obtenemos e2 = (2.71828...)2 = 7.389056...
Pero probemos con más y más términos de nuestra serie infinita:
| Términos | Resultado | |
|---|---|---|
| 1+2 | 3 | |
| 1+2+222! | 5 | |
| 1+2+222!+233! | 6.3333... | |
| 1+2+222!+233!+244! | 7 | |
| 1+2+222!+233!+244!+255! | 7.2666... | |
| 1+2+222!+233!+244!+255!+266! | 7.3555... | |
| 1+2+222!+233!+244!+255!+266!+277! | 7.3809... | |
| 1+2+222!+233!+244!+255!+266!+277!+288! | 7.3873... |
¡Empieza muy mal, pero luego mejora cada vez más!
Prueba usando "2^n/fact(n)" y n=0 hasta 20 en la Calculadora Sigma y mira lo que obtienes.
Aquí tienes algunas Series de Taylor comunes:
| Desarrollo en Serie de Taylor | En Notación Sigma |
|
ex = 1 + x + x22! + x33! + ... |
∞
Σ
n=0
xnn!
|
|
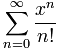sen x = x − x33! + x55! − ... |
∞
Σ
n=0
(−1)n(2n+1)!x(2n+1)
|
|
cos x = 1 − x22! + x44! − ... |
∞
Σ
n=0
(−1)n(2n)!x2n
|
|
11 − x = 1 + x + x2 + x3 + ... para |x| < 1 |
∞
Σ
n=0
xn
|
(Hay muchas más).
Aproximaciones
Podemos usar los primeros términos de una Serie de Taylor para obtener un valor aproximado de una función.
Aquí mostramos aproximaciones cada vez mejores para cos(x):
| 1 − x2/2! |  |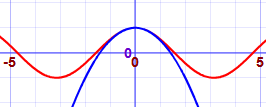
| 1 − x2/2! + x4/4! |  |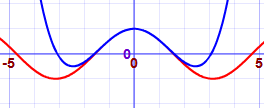
| 1 − x2/2! + x4/4! − x6/6! |  |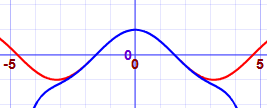
| 1 − x2/2! + x4/4! − x6/6! + x8/8! |  |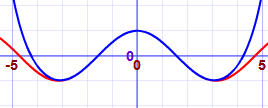
También puedes ver la Serie de Taylor en acción en laFórmula de Euler para Números Complejos.
¿Qué clase de magia es esta?
¿Cómo podemos convertir una función en una serie de términos de potencias como esta?
Bueno, no es magia realmente. Primero decimos que queremos tener este desarrollo:
f(x) = c0 + c1(x−a) + c2(x−a)2 + c3(x−a)3 + ...
Luego elegimos un valor "a", y calculamos los valores c0 , c1 , c2 , ... y así sucesivamente.
Y esto se hace usando derivadas (así que debemos conocer la derivada de nuestra función).
Repaso rápido: una derivada nos da la pendiente de una función en cualquier punto.
Estas reglas de derivación básicas nos pueden ayudar:
- La derivada de una constante es 0
- La derivada de ax es a (ejemplo: la derivada de 2x es 2)
- La derivada de xn es nxn−1 (ejemplo: la derivada de x3 es 3x2)
Usaremos la pequeña marca ' para significar "derivada de".
Bien, empecemos:
Para obtener c0, elegimos x=a para que todos los términos (x−a) se vuelvan cero, dejándonos con:
f(a) = c0
Así que c0 = f(a)
Para obtener c1, tomamos la derivada de f(x):
f'(x) = c1 + 2c2(x−a) + 3c3(x−a)2 + ...
Con x=a todos los términos (x−a) se vuelvan cero:
f'(a) = c1
Así que c1 = f'(a)
Para obtener c2, volvemos a derivar:
f''(x) = 2c2 + 3×2×c3(x−a) + ...
Con x=a todos los términos (x−a) se vuelvan cero:
f''(a) = 2c2
Así que c2 = f''(a)/2
De hecho, está surgiendo un patrón. Cada término es:
- la siguiente derivada de orden superior...
- ... dividida por todos los exponentes multiplicados entre sí hasta el momento (para lo cual podemos usar la notación factorial, por ejemplo 3! = 3×2×1)
Y obtenemos:
f(x) = f(a) + f'(a)1!(x−a) + f''(a)2!(x−a)2 + f'''(a)3!(x−a)3 + ...
Ahora tenemos una forma de encontrar nuestra propia Serie de Taylor:
Para cada término: toma la siguiente derivada, divide por n!, multiplica por (x−a)n
Ejemplo: Serie de Taylor para cos(x)
Empezamos con:
f(x) = f(a) + f'(a)1!(x−a) + f''(a)2!(x−a)2 + f'''(a)3!(x−a)3 + ...
La derivada de cos es −sen, y la derivada de sen es cos, así que:
- f(x) = cos(x)
- f'(x) = −sen(x)
- f''(x) = −cos(x)
- f'''(x) = sen(x)
- y así sucesivamente...
Y obtenemos:
cos(x) = cos(a) − sen(a)1!(x−a) − cos(a)2!(x−a)2 + sen(a)3!(x−a)3 + ...
Ahora ponemos a=0, lo cual es genial porque cos(0)=1 y sen(0)=0:
cos(x) = 1 − 01!(x−0) − 12!(x−0)2 + 03!(x−0)3 + 14!(x−0)4 + ...
Simplificamos:
cos(x) = 1 − x2/2! + x4/4! − ...
Intenta hacerlo tú mismo para sen(x), te ayudará a aprender.
O pruébalo con otra función de tu elección.
La clave es conocer las derivadas de tu función f(x).
Nota: Una Serie de Maclaurin es una Serie de Taylor donde a=0, por lo que todos los ejemplos que hemos usado hasta ahora también pueden llamarse Series de Maclaurin.
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
