Funciones Continuas
Una función es continua cuando su gráfica es una única curva ininterrumpida ...
...
que podrías dibujar sin levantar el bolígrafo del papel.
Esa no es una definición formal, pero ayuda a comprender la idea.
Aquí hay una función continua:
Ejemplos
Entonces, ¿qué no es continuo (también
llamado discontinuo)?
Busca agujeros, saltos o asíntotas verticales (donde la función se
dirige hacia arriba/abajo hacia el infinito).
 |
 |
 |
||
| No Continua |
No Continua |
No Continua |
||
| (hueco) | (salto) | (asíntota vertical) |
Prueba estas diferentes funciones para que te hagas una idea:
(Usa el control deslizante para hacer zoom, arrastra el gráfico para reposicionar y haz clic en el gráfico para volver a centrarlo).
Dominio
Toda función tiene un Dominio.
En su forma más simple, el dominio son todos los valores que entran en una función.
Es posible que podamos elegir un dominio que haga que la función sea continua.
Ejemplo: 1/(x–1)
En x=1 se tiene:
Entonces hay una "discontinuidad" en x=1
f(x) = 1/(x–1)
Por lo tanto, f(x) = 1/(x–1) en todos los números reales NO es continuo
Cambiemos el dominio a x>1
g(x) = 1/(x–1) para x>1
Así, g(x) SÍ es continua
En otras palabras, g(x) no incluye el valor x=1, por lo que es continua.
Cuando una función es continua dentro de su dominio, es una función continua.
¡Formalidad!
Podemos definir continuidad usando Límites (ayuda leer esa página primero):
Una función f es continua cuando, para cada valor c en su dominio:
f(c) está definida,
y
limx→cf(x) = f(c)
"el límite de f(x) cuando x se acerca a c es igual a f(c)"
El límite dice:
"a medida que x se acerca cada
vez más a c
se tiene que f(x) se acerca cada vez más a f(c)"
Y tenemos que comprobar desde ambas direcciones:
| cuando x se acerca a c (desde la izquierda) tenemos que f(x) se aproxima a f(c) |
 |
|
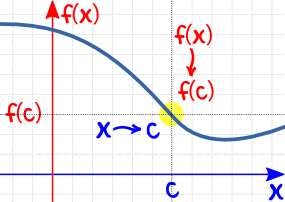| Y cuando x se acerca a c (desde la derecha) tenemos que f(x) se aproxima a f(c) |
 |
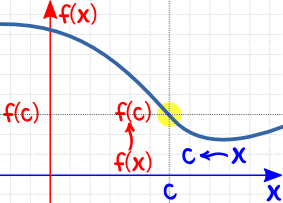Si obtenemos valores diferentes por la izquierda y la derecha (un
"salto"), ¡entonces el límite no existe!
Y recuerde que esto tiene que ser cierto para todos los valores c
del dominio.
Cómo se usa:
Asegúrate que para todos los valores de x se cumpla que:
- f(x) esté definida
- y que el límite en x sea igual a f(x)
Aquí hay algunos ejemplos:
Ejemplo: f(x) = (x2–1)/(x–1) para todos los Números Reales
La función está indefinida en x=1:
(x2–1)/(x–1) = (12–1)/(1–1) = 0/0
Entonces no es una función continua.
Cambiemos el dominio.
Ejemplo: g(x) = (x2–1)/(x–1) en el intervalo x<1
Es casi la misma función, pero ahora se encuentra en un intervalo que no incluye x = 1.Entonces ahora sí es una función continua (no incluye el "agujero")
Ejemplo: ¿Qué tal esta función definida por partes?
la cual se ve así:
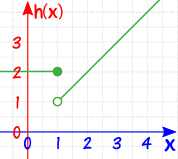
Está definida en x = 1, porque h(1)=2
(sin "agujero")
Pero en x=1 no se puede decir cuál es el límite,
porque hay dos respuestas en competencia:
- "2" desde la izquierda y
- "1" desde la derecha
entonces, de hecho, el límite no existe en x=1 (hay un "salto")
Y entonces la función no es continua.
Pero:
Ejemplo: ¿Qué hay de la función valor absoluto, la cual también está definida por partes?
¡En x=0 tiene un cambio muy puntiagudo!
Pero todavía está definida en x=0, porque f(0)=0
(por lo que no hay "agujero"),
Y el límite cuando te acercas a x=0 (desde cualquier lado) también es
0 (por lo que no hay "salto"),
Entonces, de hecho, es continua.
(Pero no lo es diferenciable).
