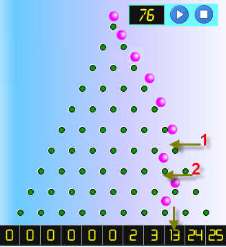
Cómo Funciona un Quincunce

Un quincunce o "tablero de Galton" (llamado así en honor de Sir Francis Galton) es una distribución triangular de clavos.

Se dejan caer bolas sobre el clavo de arriba y van rebotando hasta abajo, donde caen en pequeños contenedores.

Cada vez que una bola cae sobre un clavo, rebota a la izquierda o a la derecha.

standard normal distribution small

Pero esto es lo interesante: si siempre hay la misma probabilidad de ir a derecha o izquierda, las bolas que caen en los contenedores forman la famosa curva "de campana" de la distribución normal.

Al ser eventos aleatorios individuales, no seguirán perfectamente la curva suave de la distribución normal, pero sí tienden a hacerlo.

Fórmula

¡Podemos calcular las probabilidades!

Piensa: una bola cae en el contenedor que está a distancia k del borde derecho si ha ido a la izquierda k veces.

En este ejemplo la bola ha ido dos veces a la izquierda y todas las demás a la derecha. Acabó a distancia dos del borde derecho.

En general, si el quincunce tiene n filas, cada bola puede rebotar k veces a la izquierda y (n-k) veces a la derecha.

La probabilidad suele ser del 50% en ambos sentidos, pero podría ser del 60% - 40%, etc.

Y si la probabilidad de rebotar a la izquierda es p entonces la probabilidad de ir a la derecha es (1-p) y la probabilidad de cualquier camino se calcula así:


		La bola rebota k veces a la izquierda con probabilidad p: p^k
		Y los otros (n-k) rebotes tienen probabilidad: (1-p)^(n-k)
		Así que la probabilidad de seguir un camino así es p^k(1-p)^(n-k)

¡Pero hay muchos caminos así! Por ejemplo ir a la izquierda podría pasar en los dos primeros rebotes, o primero y tercero, o segundo y séptimo, etc.

Podrías hacer una lista y contar (IIDDD.., IDIDD..., IDDDI...), pero hay dos maneras más fáciles.

Cuántos caminos

Puedes leer sobre el Triángulo de Pascal. De hecho, el quincunce es como el triángulo de Pascal, con clavos en lugar de números. El número en cada clavo te dice cuántos caminos diferentes llegan a ese clavo. Increíble pero cierto.

O puedes usar esta fórmula para Combinaciones:

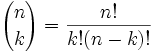			Se suele decir "n sobre k" y escribir C(n,k). Es el cálculo del número de maneras de distribuir k cosas en una sucesión de n.

			(El "!" significa "factorial", por ejemplo 4! = 1×2×3×4 = 24)

Si lo juntamos todo, la fórmula que sale es:

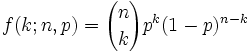
f(k;n,p) = (n en k) p^k (1-p)^(n-k)
(Por cierto, esta es la fórmula de la Distribución Binomial).

Ejemplo:

Si hay 10 filas (n=10) y la probabilidad de ir a la izquierda es 0.5 (p=0.5), podemos calcular la probabilidad de caer en el tercer contenedor por la derecha (k=3) así:

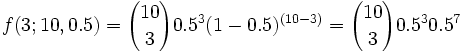
f(3;10,0.5) = (10 en 3) 0.5^3 (1-0.5)^(10-3)
también:

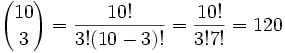
(10 en 3) = 10! / 3!(10-3)! = 120
(Esto quiere decir que hay 120 caminos diferentes que acaban
con la bola en el tercer contenedor desde la derecha.)

Así que tenemos:

De hecho, podemos hacer una tabla completa para filas=10 y probabilidad=0.5 así:

Desde la derecha:	10	9	8	7	6	5	4	3	2	1	0
Probabilidad:	0.001	0.010	0.044	0.117	0.205	0.246	0.205	0.117	0.044	0.010	0.001
Ejemplo: 100 bolas	0	1	4	12	21	24	21	12	4	1	0

Claro, este juego tiene azar así que los resultados reales no coinciden con esta situación ideal.

Otro ejemplo:

Si la probabilidad de ir hacia la izquierda fuera 0.8 la tabla quedaría así:

Desde la derecha	10	9	8	7	6	5	4	3	2	1	0
Probabilidad	0.107	0.268	0.302	0.201	0.088	0.026	0.006	0.001	0.000	0.000	0.000
Ejemplo: 100 bolas	11	26	30	20	9	3	1	0	0	0	0

Prueba tú mismo

Deja caer 100 (o más) bolas en el quincunce y a ver qué resultados salen. Yo lo he hecho muchas veces mientras escribía los programas de software. Nunca salió el resultado perfecto, pero siempre salían resultados sorprendentemente cerca. ¡Buena suerte!